Download App
જો પ્રથમ ક્રમની પ્રક્રિયા માટે $T_1 $ તાપમાને વેગ અચળાંક  $K_1 $ તથા તાપમાન  $T_2 $ એ વેગઅચળાંક  $K_2 $  હોય, તો નીચેનામાંથી કયો સંબંધ સાચો છે.? ( $E_a $ = સક્રિયકરણ ઉર્જા)
  • A$\log \,\,\frac{{{k_1}}}{{{k_2}}}\,\, = \,\,\frac{{2\,.\,\,303\,\,{E_a}}}{R}\,\,\,\left( {\frac{{{T_2} - {T_1}}}{{{T_1}{T_2}}}} \right)$
  • B$\log \,\,\frac{{{k_1}}}{{{k_2}}}\,\, = \,\,\frac{{{E_a}}}{{2.303\,R}}\,\,\,\left( {\frac{{{T_1} - {T_2}}}{{{T_1}{T_2}}}} \right)$
  • C$\log \,\,\frac{{{k_1}}}{{{k_2}}}\,\, = \,\,\frac{{2.303\,\,{E_a}}}{R}\,\,\,\left( {\frac{{{T_1}{T_2}}}{{{T_2} + {T_1}}}} \right)$
  • D$\log \,\,\frac{{{k_1}}}{{{k_2}}}\,\, = \,\frac{{{E_a}}}{{2.303\,R}}\,\,\left( {\frac{{{T_1}{T_2}}}{{{T_2} - {T_1}}}} \right)$
Easy
Download our app for free and get startedPlay store
b
પ્રથમક્રમની પ્રક્રિયા માટે આર્હેનિયસ સમીકરણ  \( k = Ae\)\(^{- Ea/RT}\)

\(\therefore \,\,\frac{{{k}_{2}}}{{{k}_{1}}}=\frac{{{e}^{-Ea/R{{T}_{1}}}}}{{{e}^{-Ea/R{{T}_{2}}}}}\)

\(={{e}^{Ea/R{{T}_{2}}-Ea/R{{T}_{1}}}}\)

\(={{e}^{\frac{{{E}_{a}}}{R}\left( \frac{1}{{{t}_{2}}}-\frac{1}{{{t}_{1}}} \right)}}\)

\(={{e}^{\frac{{{E}_{a}}}{R}\left( \frac{{{T}_{2}}-{{T}_{1}}}{{{T}_{1}}{{T}_{2}}} \right)}}\)

\(\,\therefore \,\,\,\log \,\,\frac{{{E_a}}}{{2.303\,R}}\,\,\left( {\frac{{{T_2} - {T_1}}}{{{T_1}{T_2}}}} \right)\)

art

Download our app
and get started for free

Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Download App

Similar Questions

  • 1
    આપેલ $T$  તાપમાને કેટલીક પ્રક્રિયાનો કેટલાક ક્રમ માટેનો દર અચળાંક $K$  છે તો $\mathop {\lim }\limits_{T \to \infty } \,\,\log \,\,K$...... મૂલ્ય મળશે.
    View Solution
  • 2
    પ્રથમ ક્રમની પ્રક્રિયા $A \rightarrow B$ માટે જો $K$ વેગ અચળાંક હોય અને પ્રક્રિયક $A$ ની શરૂઆતની સાંદ્રતા $0.5\, M$ હોય તો અર્ધઆયુષ્ય .............. થશે.
    View Solution
  • 3
    જો પ્રથમ ક્રમની પ્રક્રિયામાં વાયુમય પ્રક્રિયક અને વાયુમય નિપજો આવેલ હોય તો તેના દર  અચળાંક એકમ શું હશે?
    View Solution
  • 4
    $1/2 A\rightarrow 2B$ પ્રક્રિયા માટે ... સમીકરણ એ અપારદર્શક $A$ પારદર્શક $ 'B'$  નાં દર સાથે સંબંધ દર્શાવે છે.
    View Solution
  • 5
    જો પ્રક્રિયકની સાંદ્રતા $a$ હોય તો $100\%$ શૂન્યક્રમની પ્રક્રિયા પૂરી કરવા માટે કેટલો સમય લાગશે ?
    View Solution
  • 6
    ઉષ્માશોષક પ્રક્રિયા માટે, જ્યાં $\Delta H$ $kJ/mol$માં પ્રક્રિયાના એન્થાલ્પીનું પ્રતિનિધિત્વ કરે છે, સક્રિયકરણની ઊર્જા માટે ન્યૂનતમ મૂલ્ય શું હશે?
    View Solution
  • 7
    નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.

    $\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$

    પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.

    સ્ટેપ

    Rate constant $\left(\sec ^{-1}\right)$

    Activation energy 

    $\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
    $1$ ${k}_1$ $300$
    $2$ ${k}_2$ $200$
    $3$ ${k}_3$ $\mathrm{Ea}_3$

    ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).

    View Solution
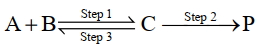
  • 8
    પ્રક્રિયા $2{N_2}{O_5} \to 4N{O_2}$ $ + {O_2}$ નો વેગ અચળાંક $3 \times {10^{ - 5}}{\sec ^{ - 1}}$ છે. જો પ્રક્રિયાનો વેગ $2.40 \times {10^{ - 5}}\,mol\,\,litr{e^{{\rm{ - 1}}}}{\sec ^{ - 1}}$ હોય, તો ${N_2}{O_5}$ ની સાંદ્રતા  ( $mol\,L^{-1}$ માં ) .............. થશે.
    View Solution
  • 9
    આપેલ પ્રક્રિયા $2NO + {O_2} \to 2N{O_2}$ કઈ પ્રક્રિયાનું ઉદાહરણ છે?
    View Solution
  • 10
    જો $75\%$  પ્રથમ ક્રમ પ્રક્રિયા $32$ મિનિટમાં પુરી થાય તો એ જ પ્રક્રિયા $50\%$ પુરી થવા કેટલી મિનિટ લાગશે.
    View Solution