જ્યારે તાપમાનમાં $27^{\circ} \mathrm{C}$ થી $57^{\circ} \mathrm{C}$ ફેરફાર થાય છે ત્યારે પ્રક્રિયાનો વેગ (દર) ચાર ગણો થાય છે. સક્રિયકરણ શક્તિની ગણાતરી કરો.
( $\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}, \log 4=0.6021$ આપેલ છે.)
NEET 2024, Medium
Download our app for free and get started
d
$ \text { Sol. } \log \left(\frac{k_2}{k_1}\right)=\frac{E_a}{2.303 R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) $
$ \text { Sol. } \log \left(\frac{k_2}{k_1}\right)=\frac{E_a}{2.303 R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) $
$ \log \left(\frac{4}{1}\right)=\frac{E_a}{2.303 R}\left(\frac{1}{300}-\frac{1}{330}\right) $
$ E_a=\frac{(\log (4)) \times 2.303 \times 8.314 \times 300 \times 330}{30} $
$ =3.804 \times 10^4 \mathrm{~J} / \mathrm{mol} $
$ =38.04 \mathrm{~kJ} / \mathrm{mol}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $75\%$ પ્રથમ ક્રમ પ્રક્રિયા $32$ મિનિટમાં પુરી થાય તો એ જ પ્રક્રિયા $50\%$ પુરી થવા કેટલી મિનિટ લાગશે.View Solution
- 2નીચે આપેલ વિધાન/નો ની સંખ્યા કે જે સાચા છે તે $......$View Solution
$A$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) ઊચી હોય છે
$B$.જો પ્રક્રિયા શૂન્ય સક્રિકરણ શક્તિ ધરાવે, તો તેનો વેગ તાપમાન થી સ્વતંત્ર છે
$C$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) નીચી હોય છે
$D$.જો તાપમાન અને વેગ અયળાંક વચ્ય જો સહસંબંધ ના હોય તો પછી તેનો ઈ અર્થ થાય છે કે પ્રક્રિયા ઋણ સક્રિયકરણ શક્તિ ધરાવે છે.
- 3રેડીયો સમસ્થાનિકની અર્ધઆયુ ચાર કલાક છે. જો સમસ્થાનિકનું શરૂઆતનું દળ $200\,g$ હોય તો $24$ કલાક પછી ....... $g$ દળ બાકી રહેશે.View Solution
- 4પ્રથમ ક્રમની પ્રક્રિયામાં પ્રક્રિયકની સાંદ્રતા $20$ મિનિટમાં $1.0\,M$ થી $0.25 \,M$ સુધી ઘટે છે. તો પ્રક્રિયાનો દર અચળાંક શું થશે?View Solution
- 5પ્રક્રિયા $A \to B$ પ્રથમ ક્રમની ગતિકીને અનુસરે છે. $A$ ના $0.8$ મોલમાંથી $B$ ના $0.6$ મોલ ઉત્પન્ન કરવા $1$ કલાક લાગે છે. તો $A$ ના $0.9$ મોલમાંથી $B$ ના $0.675$ મોલ ઉત્પન્ન કરવા .......... કલાક લાગશે .View Solution
- 6બે પ્રક્રિયાઓ $R_1$ અને $R_2$ ના પૂવઘાતાંકીય અવયવો સમાન છે. $R_1$ ની સક્રિયકરણ ઊર્જા $R_2$ કરતા $10\, kJ\,mol^{-1}$ વધારે છે. $300 \,K$ તાપમાને પ્રક્રિયાઓ $R_1$ અને $R_2$ ના વેગ અચળાંક અનુક્રમે $k_1$ અને $k_2$ હોય, તો $\ln (k_2/k_1)$ કોને સમાન થશે ?View Solution
- 7પ્રક્રિયા, $a A +b B \rightarrow c C +d D$ માટે, આલેખ $\log \,k$ વિરૂધ્ધ $\frac{1}{ T }$ ને નીચે આપેલ છેView Solution
કયા તાપમાને $(K$ માં) પ્રક્રિયાનો વેગ અચળાંક $10^{-4} s ^{-1}$ થશે તે શોધો ?(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)
[આપેલ : $500\, K$ પર, પ્રક્રિયાનો વેગ અચળાંક $10^{-5} s^{-1}$ છે.]
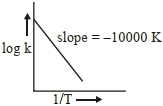
- 8પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે જ્યારે $\log \,k$ વિરૂદ્ધ $1/T $ નો આલેખ આપેલ છે. જેનો ઢાળ $-8000 $ સીધી રેખામાં મળે છે,તો પ્રક્રિયાની સક્રીયકરણ ઊર્જા ......... $cal$ શોધો.View Solution
- 9View Solutionઅથડામણના સિધ્ધાંત મુજબની નીચેના પૈકી કયું વિધાન સાચું નથી. ?
- 10પ્રક્રિયા માટેનો દર અચળાંક $10.8 × 10^{-5 }$ મોલ $L^{-1 } S^{-1 } $ છે. તો પ્રક્રિયા ....... થાય.View Solution