किसी प्रिज्म का कोण $A$ है। इस प्रिन्म के एक अपवर्तक फलक को रजतित कर परावर्तक बना दिया गया है, इसके पृष्ठ पर, $2 A$ कोण पर आपतित प्रकाश की किरणें, रजतित फलक से परावर्तन के पश्चात् अपने मार्ग पर वापस आ जाती हैं। प्रिज्म के पदार्थ का अपवर्तनांक $\mu$ होगा
[2014]
Download our app for free and get started
प्रश्नानुसार निम्न किरण रेखाचित्र परिवर्तन करेगा।
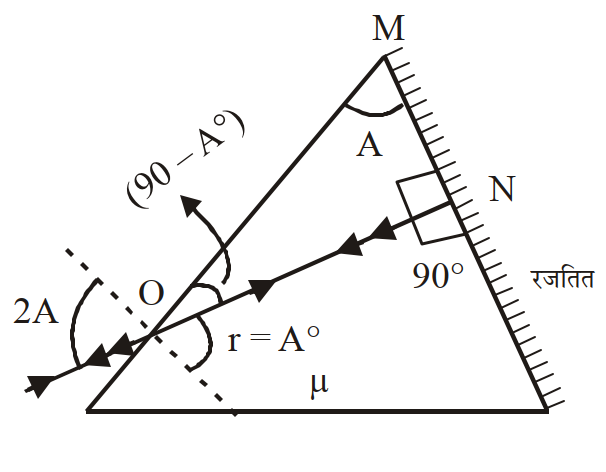
$ \angle MON =90- A ^{\circ}$
$\angle r =90-90+ A ^{\circ}= A ^{\circ} $
स्नेल के नियम से, $\frac{\sin i}{\sin r}=\mu$
चित्र से,
$ \angle i =2 A $
$\angle r = A$
$\mu=\frac{\sin 2 A }{\sin A }$
$=\frac{2 \sin A \cos A }{\sin A }$
$\mu=2 \cos A $
$ \angle MON =90- A ^{\circ}$
$\angle r =90-90+ A ^{\circ}= A ^{\circ} $
स्नेल के नियम से, $\frac{\sin i}{\sin r}=\mu$
चित्र से,
$ \angle i =2 A $
$\angle r = A$
$\mu=\frac{\sin 2 A }{\sin A }$
$=\frac{2 \sin A \cos A }{\sin A }$
$\mu=2 \cos A $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$f _1$ और $f _2$ फोकस दूरियों के दो पतले लैंस अक्षीय रूप से जुड़े हुए हैं। इस युग्म की शक्ति (पावर) होगी :View Solution
- 2$5000 A$ तरंगदैर्ध्य पर $10$ सेमी व्यास के अभिदृश्यक युक्त दूरदर्शी के कोणीय विभेदन का क्रम है:View Solution
- 3प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{3}$ है। न्यूनतम विचलन कोण का मान होगा :View Solution
- 4एक विद्युत चुम्बकीय तरंगों की आवृत्ति, $n$ तथा तरंग दैर्ध्य $\lambda$ है । यह हवा में $v$ वेग से चलता हुआ $\mu$ अपवर्तनांक वाले काँच में जाता है। कांच में इसकी आवृत्ति, तरंगदैधर्य तथा वेग ज्ञात करोView Solution
- 5प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{2}$ तथा इसका अपवर्तन कोण $30^{\circ}$ है। प्रिज्म के अपवर्तक पृष्ठों में से किसी एक पृष्ठ को अन्दर की ओर दर्पणनुमा बनाया जाता है। दूसरे पृष्ठ पर आपतित एकवर्णी प्रकाश पुँज दर्पण से परावर्तित होकर अपने ही मार्ग से वापिस लौट आएगा यदि प्रिज्म पर आपतन कोण है:View Solution
- 6किसी खगोलीय दूरबीन के अभिदृश्यक और नेत्रिका की फोक्स दूरियां कमश: $40$ से.मी. और $4$ से.मी. हैं। अभिदृश्यक से $200$ से.मी. दूर स्थित किसी बिम्ब को देखने के लिए दोनों लेंसों के बीच की दूरी होनी चाडिए:View Solution
- 7$60^{\circ}$ के किसी प्रिज्म पर प्रकाश की एक किरण अल्पतम् विचलन की स्थिति पर आपतित होती है। पहले पाश्र्व (फलक) पर (अर्थात् आपतन पाश्र्व पर) अपवर्तन कोण हैView Solution
- 8View Solutionएक उत्तल लैंस को ऐसे द्रव में डुबोया जाता है, जिसका अपवर्तनांक लैंस के पदार्थ के अपवर्तनांक के बराबर है तो इसकी फोकस दूरी होगी:
- 9एक लेंस, प्रकाश स्रोत्र तथा दीवार के बीच रखा है। यह लेंस के दो भिन्न स्थितियों दीवार पर $A _1$ तथा $A _2$ क्षेत्रफल के दो प्रतिबिम्ब बनाता है। प्रकाश स्रोत्र का क्षेत्रफल होगाView Solution
- 10एक दूरदर्शी यंत्र का आवर्धन क्षमता $9$ है। जब इसे समान्तर किरणों के लिए समायोजित किया जाता है तब इसके अभिदृश्यक तथा नेत्रिका के बीच की दूरी $20 \ cm$ होती है। इन लेंसों की फोकस दूरियाँ क्रमश होगी:View Solution