કણ નિયમિત વર્તૂળાકાર ગતિ $L$ જેટલા કોણીય વેગમાનથી કરે છે. જો તેની કોણીય આવૃત્તિ બમણી અને ગતિ ઊર્જા અડધી કરવામાં આવે ત્યારે નવું કોમીય વેગમાન કેટલું થશે ?
AIEEE 2003, Diffcult
d
કોણીય વેગમાન \({\text{L = I }}\omega \)
કોણીય વેગમાન \({\text{L = I }}\omega \)
ચકગતિ ઉર્જા \({E_K} = \,\,\frac{1}{2}\,\,I{\omega ^2}\,\)
\(\therefore \,\,\frac{L}{{{E_K}}}\,\, = \,\,\frac{{I\omega }}{{\frac{1}{2}\,I{\omega ^2}}}\,\, = \,\,\frac{2}{\omega }\,\,\,\,\,\therefore \,\,L\,\, = \,\,\frac{2}{\omega }\,\,{E_K}\)
આથી \(\,\frac{{{L_1}}}{{{L_2}}}\,\, = \,\,\,\frac{{2\,{E_{K1}}}}{{{\omega _1}}}\,\, \times \,\,\,\frac{{{\omega _2}}}{{2{E_{k2}}}}\,\,\, = \,\,\,\frac{{{E_{K1}}}}{{{E_{K2}}}}\,\,\, \times \,\,\,\frac{{{\omega _2}}}{{{\omega _1}}}\,\,\,\,\)
\( = \,\,\frac{{{E_{K1}}}}{{\frac{{{E_{K1}}}}{2}}}\,\, \times \,\,\frac{{2{\omega _1}}}{{{\omega _1}}}\,\,\,\,\, = \,\,2\,\, \times \,\,2\,\,\,\, = \,\,4\)
\(\therefore \,\,\,{L_2} = \,\,\frac{{{L_1}}}{4}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
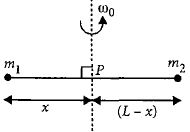
- 1View Solutionઆકૃતિમાં કઇ અક્ષ પર કોણીય પ્રવેગ વધુ થશે અને બળ ત્રિકોણ ફ્રેમના મધ્યબિંદુ પર લાગે છે.
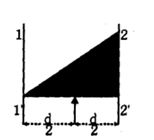
- 2$m_1$ અને $m_2$ ના બે બિંદુવત દળને દઢ $L$ લંબાઈ અને નહિવત દળ ધરાવતા સળીયાના સામસામેના છેડે રાખવામાં આવેલાં છે. આ સળિયાને લંબરૂપે રહેલી અક્ષને અનુલક્ષીને ભ્રમણ કરે છે. આ અક્ષ પર રહેલા બિંદુ $P$ નું એવું સ્થાન મેળવો કે જેના માટે સળિયો કોણીય વેગમાન ${\omega _0}$ થી પરિભ્રમણ કરે, ત્યારે જરૂરી કાર્ય ન્યુનતમ થાય?View Solution
- 3View Solutionએક નિશ્ચિત બિંદુની આસપાસ સમતલમાં કોઈ દળ ભ્રમણ કરે છે, તેનું કોણીય વેગમાન કઈ દિશામાં હશે?
- 4પદાર્થ પર ટોર્ક લગાડ્યા વગર તેની કોણીય ઝડપમાં થતો ફેરફાર $\omega_1$ થી $\omega_2$ છે. જે તેની જડત્વની ચાકમાત્રાને લીધે થાય છે. તો બંને કિસ્સામાં ચક્રાવર્તનની ત્રિજ્યાઓનો ગુણોત્તર =…..View Solution
- 5View Solutionએક પાતળી સમક્ષિતિજ તકતી તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને ચાકગતિ કરે છે. એક જંતુ એ તકતીના વ્યાસ પર એક છેડેથી સામેના બીજા છેડે ગતિ કરે છે. તો તેની ગતિ દરમિયાન તકતીની કોણીય ઝડપ.....
- 6$m$ દળ અને $l$ લંબાઇ ધરાવતા સળિયાના મધ્યબિંદુ અને છેડાની મધ્યમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 7એક તક્તી $\vec{\omega}$ કોણીય ઝડપથી ભ્રમણ કરી રહી છે. બ્રમણાક્ષની સાપેક્ષે સ્થાન સદિશ $\vec{r}$ ધરાવતાં બિંદુ પર $\vec{F}$ બળ લગાડવામાં આવે છે. તો આ બળ વડે ઉદભવતાં ટોર્કની સાથે જોડાયેલો પાવર શું થશે ?View Solution
- 8View Solutionપાતળી પોલો નળાકાર બંનેને છેડેથી ખુલ્લો છે. તે રોલિંગ કર્યા વિના સરકે છે અને પછી સરક્યા વિના તેટલી જ ઝડપથી રોલિંગ કરે છે બંને કિસ્સામાં ગતિ ઊર્જાનો ગુણોત્તર ........ થશે.
- 9View Solutionપૃથ્વી તેની અક્ષ પર ભ્રમણ કરે છે તે બાબતે....
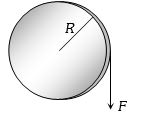
- 10$R$ ત્રિજયા અને $M$ દળ ધરાવતી તકતી તેના કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને ચાકગતિ કરી શકે છે.તેના પર સ્પર્શીય બળ $F$ લગાડતાંં સ્પર્શીય પ્રવેગView Solution