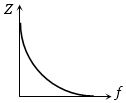
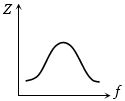
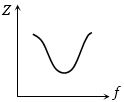
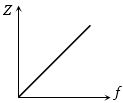
$LCR$ શ્રેણી પરિપથનો ઇમ્પિડન્સ $(Z)$ વિરુધ્ધ આવૃત્તિ $f$ નો આલેખ કેવો થાય?
Medium
c
(c) \(Z = \sqrt {{R^2} + {{\left( {2\pi fL - \frac{1}{{2\pi fC}}} \right)}^2}} \)
(c) \(Z = \sqrt {{R^2} + {{\left( {2\pi fL - \frac{1}{{2\pi fC}}} \right)}^2}} \)
From above equation at \(f\) = \(0\) \( \Rightarrow z = \infty \)
When \(f = \frac{1}{{2\pi \sqrt {LC} }}\) (resonant frequency) \( \Rightarrow Z = R\)
For \(f > \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow \) \( Z\) starts increasing.
i.e., for frequency \(0 -\) \(fr\), \(Z\) decreases and for fr to \(\infty\), \(Z\) increases. This is justified by graph \(c\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
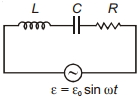
- 1એક $LCR$ શ્રેણી પરિપથ, $\varepsilon=\varepsilon_0 \sin \omega t$. $emf$ ના સ્ત્રોત સાથે જોડેલ ઈન્ડકટર $L$, કેપેસિટર $C$ અને અવરોધ $R$નો બનેલો છે.જ્યારે $\omega L=\frac{1}{\omega C}$ ત્યારે પરિપથમાં વિદ્યુતપ્રવાહ $I_0$ છે અને જો સ્ત્રોતની કોણીય આવૃત્તિ $\omega^{\prime}$, માં બદલવામાં આવે, તો પરિપથમાં વિદ્યુતપ્રવાહ $\frac{I_0}{2}$, થાય છે,તો $\left|\omega^{\prime} L-\frac{1}{\omega^{\prime} C}\right|$ નું મૂલ્ય કેટલું છે ?View Solution
- 2$LCR$ શ્રેણી પરિપથમાં $R=10 \Omega, X_L=8 \Omega$ અને $X_C=$ $6 \Omega$ પરિપથનો કુલ ઈમ્પિડન્સ ...... $\Omega$ છે.View Solution
- 3$LCR$ પરિપથમાં અવરોધનું મૂલ્ય વધારતાView Solution
- 4$RL$ પરિપથમા પ્રવાહ $i = 100\sin 314\,t\,amp$ અને વોલ્ટેજ $e = 200\sin \,(314\,t + \pi /3)V$ છે. જો અવરોધ $1\Omega$ હોય તો રીએટન્સ કેટલો થાય?View Solution
- 5$AC$ પરિપથમાં પ્રવાહ અને વોલ્ટેજ વચ્ચેનો કળા-તફાવત $\frac{\pi }{2}$ છે.નીચે દર્શાવેલ કયો વિકલ્પ આ પરિપથ નહિ હોય?View Solution
- 6$AC$ ઉદ્ગમનો વોલ્ટેજ સમય $V = 120\sin \,100\,\pi \,t\cos\, 100\pi \,t.$ સાથે મુજબ બદલાય છે,તો મહત્તમ વોલ્ટેજ અને આવૃત્તિ કેટલી થાય?View Solution
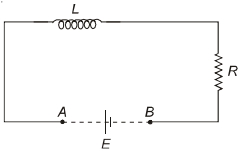
- 7એક ઇન્ડકટર $(L=100\; mH)$ અવરોધ $(R =100\;\Omega)$ અને બેટરી $(E=100\; V)$ ને શરૂઆતમાં આકૃતિમાં દર્શાવ્યા પ્રમાણે શ્રેણીમાં જોડેલાં છે. ઘણા લાંબા સમય પછી $A$ અને $B$ શૉટસર્કિટ થતાં બેટરી દૂર થઈ જાય છે, તો શૉટસર્કિટ પછી પરિપથમાંથી $1\;ms$ પછી પસાર થતો પ્રવાહ $I$ ($A$ માં) કેટલો હશે?View Solution
- 8$ R-L $ શ્રેણી પરિપથમાં અવરોધ અને ઇન્ડકટર વચ્ચેનો વોલ્ટેજ અનુક્રમે $200\,V$ અને $150\,V$ હોય,તો $ A.C.$ વોલ્ટેજ કેટલા .......$V$ થાય?View Solution
- 9કોઈક ક્ષણે એક ઉલટસૂલટ ($ac$) પ્રવાહ નીચે મુજબ આવી શકાયView Solution
$i=[6+\sqrt{56} \sin (100 \pi \mathrm{t}+\pi / 3)] \mathrm{A}$ પ્રવાહનું $rms$ મૂલ્ય. . . . . . .$A$ હશે.
- 10$10 \sqrt{3}\; \Omega$ અવરોધ, $40\; \Omega$ કેપેસિટિવ રિએકટન્સ અને $30 \Omega$ ઈન્ડકટિવ રિએકટન્સના શ્રેણી પરિપથમાં $220\,V$ નો ઓલ્ટરનેટિંગ વિદ્યુતસ્થિતિમાન લગાવેલ છે. શૂન્ય અને અનંત આવૃત્તિ માટે પરિપથમાં વિદ્યુતપ્રવાહ અનુક્રમે કટલો છે?View Solution