$m = 0.1\,kg$ દળ નો એક બ્લોક અજ્ઞાત સ્પ્રિંગ અચળાંક $k$ ધરાવતી એક સ્પ્રિંગ સાથે જોડેલી છે. જેને તેની સમતોલ અવસ્થામાથી $x$ અંતર જેટલી દબાવેલી છે. સમતોલન સ્થિતિ ના અડધા અંતરે $(\frac {x}{2})$ પહોચ્યાં બાદ, તે બીજા બ્લોક સાથે અથડાઇ ને સ્થિર થાય છે, જ્યારે બીજો બ્લોક $3\,ms^{-1}$ વેગ થી ગતિ કરે છે. તો સ્પ્રિંગ ની પ્રારંભિક ઉર્જા કેટલા ................ $\mathrm{J}$ હશે?
JEE MAIN 2015, Diffcult
b
Applying momentum conservation
Applying momentum conservation
\({m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}\)
\(0.1 u + m(0) = 0.1 (0) + m(3)\)
\(0.1 u = 3m\)
\(\frac{1}{2}0.1{u^2} = \frac{1}{2}m{\left( 3 \right)^2}\)
Solving we get, \(u = 3\)
\(\begin{gathered}
\frac{1}{2}k{x^2} = \frac{1}{2}K{\left( {\frac{x}{2}} \right)^2} + \frac{1}{2}\left( {0.1} \right){3^2} \hfill \\
\Rightarrow \,\,\,\,\frac{3}{4}k{x^2} = 0.9 \hfill \\
\Rightarrow \,\,\,\,\frac{3}{2} \times \frac{1}{2}k{x^2} = 0.9 \hfill \\
\therefore \,\,\frac{1}{2}K{x^2} = 0.6\,J\,\left( {total\,initial\,energy\,of\,the\,spring} \right) \hfill \\
\end{gathered} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
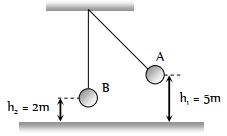
- 1ગોળો B પાસે આવે ત્યારે તેનો વેગ.....$ m/s$View Solution
- 2$5 \times {10^3}N/m$ બળ અચળાંક ધરાવતી સ્પિંગ્રની લંબાઇ $ 5 cm$ થી $10 cm$ વધારતાં થતું કાર્ય......$N-m$View Solution
- 3$4m$ દાળનો બોમ્બ $x-y$ સમતલમાં સ્થિર પડેલો છે. તે એકાએક ત્રણ ટુકડામાં વિસ્ફોટ પામે છે. બે દરેક $m$ દળના ટૂકડાઓ એકબીજાને લંબરૂપે સમાન ઝડપ $v$ થી ગતિ કરે છે. વિસ્ફોટના કારણે ઉત્પન્ન થતી કુલ ગતિઊર્જાનું મૂલ્ય ($mv^2$ માં) કેટલું હશે?View Solution
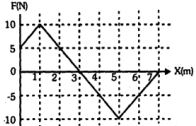
- 4પ્રારંભમાં સ્થિર સ્થિતિ એ રહેલા $m = 2kg$ દળના કણનો બળ $(F)$ વિરૂદ્ધ સ્થાનાંતરણનો આલેખ આકૃતિમાં દર્શાવ્યો છે.View Solution
$(1)$ કણની ઝડપ મહત્તમ $x = ..... m$ અંતરે થશે.
$(2) $ કણની મહત્તમ ઝડપ ...... $ms^{-1}$ છે.
$(3) $ કણ ઝડપ ફરીથી $x = .... m $ સ્થાને શૂન્ય થશે.
- 5$M$ દળ એ $m$ દળ કરતાં ઘણો વધારે છે. $M$ દળનો ભારે પદાર્થ $v$ વેગથી સ્થિર $m$ દળના હલકા પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. તો અથડામણ પછી હલકા પદાર્થનો વેગ કેટલો થશે?View Solution
- 6એક કણ પર $F=(5 y+20) \hat{j} \,N$ જેટલું બળ લાગે છે. આ બળ દ્વારા કણ $y=0 \,m$ થી $y=10 \,{m}$ સુધી સ્થાનાંતર કરવા માટે કેટલું કાર્ય (${J}$ માં) કરવું પડે?View Solution
- 7એક $m$ દળવાળી કાર એ એવું એન્જિન ધરાવે છે જે $P$ જેટલો પાવર પૂરો પાડી શકે છે. તો કારએ કેટલાં ન્યૂનતમ સમયમાં સ્થિર સ્થિતિમાંથી $v$ જેટલી ઝડપ સુધી પ્રવેગિત થઈ શકે છે તે...View Solution
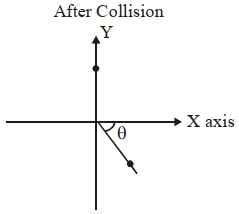
- 8$10\, kg$ દળ ધરાવતો દડો $10 \sqrt{3}\, ms ^{-1}$ ના વેગથી $X-$ અક્ષ પર ગતિ કરે છે. તે બીજા સ્થિર રહેલા $20\, kg$ દળાના દડાને અથડાય છે. અથડામણ પછી પ્રથમ દડો સ્થિર થાય છે અને બીજો દડાના બે સમાન ટુકડા થાય છે. એક ટુકડો $10\, m / s$ ના વેગથી $Y-$ અક્ષ પર ગતિ કરે છે અને બીજો ટુકડો $X-$અક્ષ સાથે $\theta$ ના ખૂણે $20\, m / s$ ના વેગથી ગતિ કરે છે. તો $\theta$ નું મૂલ્ય કેટલું હશે?View Solution
- 9$6.4\,m$ ત્રિજયા ધરાવતા પોલા ગોળાની અંદર, નીચેના બિંદુથી બાઇકને એક પરિભ્રમણ પૂરું કરવા માટે જરૂરી લઘુત્તમ વેગ .......... $m/s$ હશે.View Solution
- 10એક પદાર્થનું વેગમાંન $50 \%$ જેટલું વધારવામાં આવે છે. પદાર્થની ગતિઊર્જામાં થતો વધારો ટકાવારીમાં $.......\%$ છે.View Solution
