આપેલ : ${m}=8 \,{kg}, {M}=16\, {kg}$
આકૃતિમાં દર્શાવેલ બધી જ સપાટી ઘર્ષણરહિત ધારો.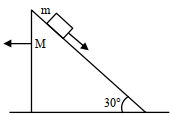
Let acceleration of wedge is \(a_{1}\) and acceleration of block w.r.t. wedge is \(a_{2}\)
\({N} \cos 60^{\circ}={Ma}_{1}=16 {a}_{1}\)
\(\Rightarrow {N}=32 {a}_{1}\)
F.B.D. of block w.r.t wedge
\(\perp\) to incline
\({N}=8 {g} \cos 30^{\circ}-8 {a}_{1} \sin 30^{\circ} \Rightarrow 32 {a}_{1}=4 \sqrt{3} {g}-4 {a}_{1}\)
\(\Rightarrow {a}_{1}=\frac{\sqrt{3}}{9} {g}\)
Along incline
\(8 g \sin 30^{\circ}+8 a_{1} \cos 30^{\circ}=m a_{2}=8 a_{2}\)
\(a_{2}=g \times \frac{1}{2}+\frac{\sqrt{3}}{9} g \cdot \frac{\sqrt{3}}{2}=\frac{2 g}{3}\)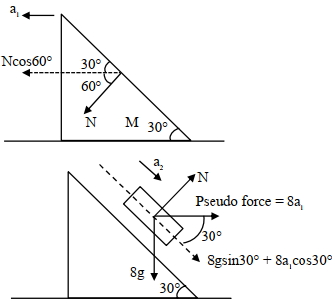
Download our appand get started for free
Similar Questions
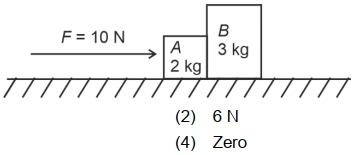
- 1આક્રુતિમાં દર્શાવ્યા અનુસા૨ $A$ બ્લોક્ને $10 N$ નું સમક્ષાતિજ બળ લગાડવામાં આવે છે. બ્લોક $A$ અને $B$ નાં દળો અનુક્રમે $2 \mathrm{~kg}$ અને $3 \mathrm{~kg}$ છે. બ્લોક ઘર્ષણરહિત સપાટી પર સરકે છે. બ્લોક $A$ દ્વારા બ્લોક $B$ પર લાગતું બળ. . . . . . . .છે.View Solution
- 2View Solutionબળની ભૌતિક સ્વતંત્રતા કોના પર આધારિત છે?
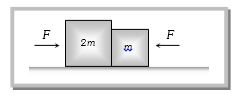
- 3View Solutionબળ વારાફરતી આકૃતિમાં દર્શાવ્યા પ્રમાણે લગાવતાં બંને બ્લોક વચ્ચેના સંપર્કબળનો ગુણોત્તર કેટલો થાય?
- 4આકૃતિમાં દર્શાવ્યા અનુસાર ઘર્ષણરહિત સપાટી પર $4\; kg,2\; kg $ અને $1\; kg$ દળના અનુક્રમે ત્રણ બ્લોક્ $A,B$ અને $C$ એકબીજાના સંપર્કમાં મૂકેલા છે. જો $4\; kg$ ના બ્લોક્ પર $14\; N$ નું બળ લગાડવામાં આવે, તો $A$ અને $B$ વચ્ચેનું સંપર્કબળ ($N$ માં) કેટલું હશે?View Solution

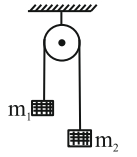
- 5એક જડિત આધાર પર લટકાવેલ લીસી પુલી પરથી પસાર થતી દોરીના છેડે $m_1$ અને $m_2$ દળ ધરાવતા બે બ્લોક જોડેલા છે. જો તંત્રનો પ્રવેગ $g / 8$ હોય તો બ્લોકના દળનો ગુણોત્તર ........View Solution
- 6નીચે મુજબ બે કથન આપેલ છે.View Solution
કથન $I$ : લીફટ ઉપર અથવા નીચેની તરફ સમાન ઝડપથી જઈ શકશે જ્યારે તેનુ વજન તેના કેબલના તણાવબળ સાથે સંતુલનમાં હોય.
કથન $II$ : લીફટના તળિયા દ્વારા તેમા ઉભી રહેલ વ્યક્તિના પગ પર લાગતું બળ તેના વજન કરતા વધુ હોય જ્યારે લીફટ વધતી જતી ઝડપથી નીચે તરફ જતી હોય.
બંને કથનના સંદર્મમાં, નીચે આપેલ વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરી.
- 7$100 \,kg$ ના દળની કાર $5 \,m/sec$ વેગથી ગતિ કરે છે.તેને $\frac{1}{{10}}\,sec$ સમયમાં સ્થિર કરવા માટે ........ $N$ બળ લગાવવું પડે.View Solution
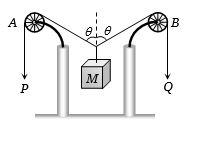
- 8આકૃતિમાં બતાવ્યા પ્રમાણે ખેંચી ન શકાય તેવી સ્પ્રિંગ ના છેડાઓ $P$ અને $Q$ નિયમિત ઝડપ $ U$ થી નીચે તરફ ગતિ કરે છે. ગરગડીઓ $A$ અને $B$ ને સ્થિત કરેલી છે. તો દળ $M$ એ ઉપર તરફ કેટલી ઝડપે ગતિ કરશે?View Solution
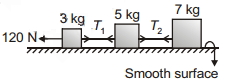
- 9આપેલી આકૃતિમાં $T_1$ અને $T_2$ મુલ્ય શું છે?View Solution
- 10એક ઝાડની ડાળી પરથી $10 \mathrm{~kg}$ દળ ધરાવતી સાંકડ વડે $200 \mathrm{~N}$ વજન ધરાવતી વસ્તુને લટાકવામાં આવે છે. ઝાડની ડાળી (શાખા) ચેઈનને. . . . . . બળ થી ખેચશે.View Solution
$\text { ( } g=10 \mathrm{~m} / \mathrm{s}^2 $ લો.)
