$m$ દળનો ઉપગ્રહએ $d$ ધનતા વાળાં ગ્રહની સપાટીની એકદમ નજીક આવર્તકાળ $T$ સાથે ભ્રમણ કરી રહ્યો છે. તો ગ્રહ પર સાર્વત્રિક ગુરુત્વાકર્ષણ અચળાંકનું મૂલ્ય શેના વડે આવવામાં આવશે ?
Medium
Download our app for free and get started
d
(d)
(d)
Time period of a satellite revolving close to surface,
\(T=\frac{2 \pi R}{v}=\frac{2 \pi R^{3 / 2}}{\sqrt{G M}}\)
\(T^2=\frac{4 \pi^2 R^3}{G M}\)
\(M=\frac{4}{3} \pi R^3 \times d\)
\(T^2=\frac{4 \pi^2 R^3}{G \frac{4}{3} \pi R^3 d}\)
\(G=\frac{3 \pi}{d T^2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન દળ ધરાવતા બે ગ્રહો $A$ અને $B$ ને તેમના પરિભ્રમણના આવર્તકાળ $T_{A}$ અને $T_{B}$ એવા છે કે $T _{ A }=2 T _{ B }$ થાય. આ ગ્રહો અનુક્રમે $r _{ A }$ અને $r _{ B }$ જેટલી ત્રિજ્યા ધરાવતી વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે. તેમની કક્ષાઆ માટે કયો સંબંધ સાચો છે ?View Solution
- 2જો પૃથ્વી પરનાં સમગ્ર દળને અનંત સુધી દૂર કરવું હોય, કે જેથી તેને સંપૂર્ણ રીતે તોડી શકાય, તો આપવી પડતી ઊર્જાનો જથ્થો$\frac{x}{5}\, \frac{ GM ^{2}}{ R }$ છે, જ્યાં $x$ ..... હશે. (નજીકતમ પૂર્ણાકમાં લખો)View Solution
($M$ એ પૃથ્વીનું દળ, $R$ એ પૃથ્વીની ત્રિજ્યા, $G$ ગુરુત્વાકર્ષી અચળાંક છે.)
- 3જો પૃથ્વીનું દળ $P$ ગ્રહ કરતાં નવ ગણું અને ત્રિજ્યા બમણી છે. તો ગ્રહ $P$ ના ગુરુત્વાકર્ષણ બળમાંથી બહાર કાઢવા માટે રોકેટ દ્વારા જરૂરી લઘુત્તમ વેગ $\frac{v_e}{3} \sqrt{x}\; ms ^{-1}$ છે. જ્યાં $v_e$ નિષ્ક્રમણ વેગ છે. $x$ ની કિંમત કેટલી હશે?View Solution
- 4સૂર્યની આજુબાજુ ભ્રમણ કરતાં ગ્રહની કોણીય વેગમાન $J$ હોય,તો ગ્રહનો ક્ષેત્રીય વેગ કેટલો થાય?View Solution
- 5વિષુવવૃત થી ધ્રુવ પર જતા $g$ નું મૂલ્યView Solution
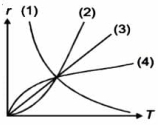
- 6ક્યો આલેખએ ઉપગ્રહની વર્તુળાકાર કક્ષાની ત્રિજ્યા $r$ માં તેના આવર્તકાળ $T$ સાથે થતો ફેરફાર સારી રીતે રજૂ કરે છે ?View Solution
- 7નીચેનામાંથી કોને સૌપ્રથમ $G$ નું પ્રાયોગિક મૂલ્ય આપ્યું?View Solution
- 8$r < R$ પાસે ગુરુત્વ પ્રવેગ નું મૂલ્ય ? જ્યાં $R=$ પૃથ્વી ની ત્રિજ્યા $r=$ પૃથ્વીના કેન્દ્રથી અંતરView Solution
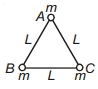
- 9દરેકનું દળ $M$ હોય એવા ત્રણ કણો $A, B$ અને $C$ એ $L$ બાજુ વાળા સમબાજુ ત્રિકોણનાં શિરોબિંદુઓ પર રહેલા છે. જો $B$ અને $C$ કણોને સ્થિર રાખીને $A$ કણને મૂક્ત કરવામાં આવે, તો $A$ નાં તત્કાલિન પ્રવેગનું મૂલ્ય શું હશે ?View Solution
- 10જો પૃથ્વીની કક્ષીય ત્રિજ્યા અત્યારની ત્રિજ્યા કરતાં $\frac{1}{4} $ ગણી થાય તો $1$ વર્ષ કેટલું થાય ?View Solution