Applying momentum conservation
\(\frac{m}{2} \times V_{0}+\frac{m}{3} \times(0)=\frac{m}{2} V_{A}+\frac{m}{3} V_{B}\)
\(=\frac{V_{0}}{2}=\frac{V_{A}}{2}+\frac{V_{B}}{3}\) \(....(1)\)
since, collision is elastic \(( e =1)\)
\(e =1=\frac{ V _{ B }- V _{ A }}{ V _{0}} \Rightarrow V _{0}= V _{ B }- V _{ A } \ldots(2)\)
On solving \((1) \&(2): V_{A}=\frac{V_{0}}{5}\)
Now, \(De-\)Broglie wavelength of \(A\) before collision :
\(\lambda_{0}=\frac{ h }{ m _{ A } V _{0}}=\frac{ h }{\left(\frac{ m }{2}\right) V _{0}}\)
\(\Rightarrow \lambda_{0}=\frac{2 h }{ mV _{0}}\)
Final \(De-\)Broglie wavelength :
\(\lambda_{ f }=\frac{ h }{ m _{ A } V _{0}}=\frac{ h }{\frac{ m }{2} \times \frac{ V _{ o }}{5}} \Rightarrow \lambda_{ f }=\frac{10 h }{ mV _{ o }}\)
Now \(\Delta \lambda=\lambda_{f}-\lambda_{0}\)
\(\Delta \lambda=\frac{10 h }{ mV _{0}}-\frac{2 h }{ mV _{0}}\)
\(\Rightarrow \Delta \lambda=\frac{8 h }{ mv _{0}} \Rightarrow \Delta \lambda=4 \times \frac{2 h }{ mv _{0}}\)
\(\Rightarrow \Delta \lambda=4 \lambda_{0}\)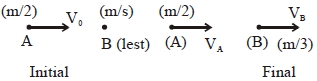
Download our appand get started for free
Similar Questions
- 1View Solutionસમાન વેગથી ગતિ કરતાં પ્રોટોન અને ન્યુટ્રોન ની દ બ્રોગ્લી તરંગ લંબાઈનો ગુણોત્તર કેટલો છે?
- 2ટંગસ્ટનની થ્રેસોલ્ડ તરંગ લંબાઈ $2300\ \mathring A$ છે. જો તેના પર આપાત થતાં પાર જાંબલી પ્રકાશની તરંગ લંબાઈ $1800\ \mathring A$ હોય તો ફોટો ઈલેક્ટ્રોનની મહત્તમ ગતિ ઊર્જા ............ $eV$ થશે.View Solution
- 3View Solutionનીચેનામાંથી કયું પ્રકાશની કણ પ્રકૃતિ દર્શાવે છે?
- 4પ્રયોગમાં આપાત વિકિરણની તરંગ લંબાઈને $6000\ Å$ થી $4000\ Å$ સુધી ઘટાડવામાં આવે ત્યારે વિકિરણની તીવ્રતા અચળ રહે છે અને .......View Solution
- 5$25\,W\,cm^{-2}$ ઉર્જાપ્રવાહ ધરાવતો પ્રકાશ સંપૂર્ણ શોષક સપાટી પર લંબરૂપે આપાત કરવામાં આવે છે,સપાટીનું ક્ષેત્રફળ $25\,cm^2$ હોય તો $40\,min$ માં સપાટીને મહત્તમ કેટલું વેગમાન મળશે?View Solution
- 6જ્યારે $hv$ ઊર્જાનો ફોટોન એલ્યુમિનિયમ ની પ્લેટ પર આપાત થાય (કાર્ય વિધેય $E_0$) ત્યારે મહત્તમ ગતિ ઊર્જા $K$ ધરાવતા ફોટો ઈલેક્ટ્રોન બહાર નીકળે છે. જ્યારે $2hv$ ઊર્જાનો ફોટોન એલ્યુમિનિયમ ની પ્લેટ પર આપાત થાય ત્યારે બહાર નીકળતાં ફોટો ઈલેક્ટ્રોનની મહત્તમ ગતિ ઊર્જા કેટલી હશે?View Solution
- 7ફોટોઈલેકિટ્રક અસર માટેનું આઈન્સ્ટાઈનનું સમીકરણ $E_k = hf - \phi_0$ છે. આ સમીકરણમાં $E_k$ ........... દર્શાવે છે.View Solution
- 8એક બિંદુ આગળ પ્રકાશ તરંગ સાથે સંકળાયેલ વિદ્યુત ક્ષેત્ર નીચે મુજબ આપી શકાય છે.View Solution
$E=200\left[\sin \left(6 \times 10^{15}\right) t+\sin \left(9 \times 10^{15}\right) t\right]^{-1}$ જો આ પ્રકાશ $2.50 \,eV$, જેટલું કાર્યવિધેય ધરાવતી ધાતુની ગતિઉર્જા ...........$eV$ હશે. (Given : $h=4.14 \times 10^{-15} \,eVs$)
- 9ઈલેકટ્રોનના વેગમાનમાં ફેરફાર $ \Delta p $ થવાથી દ-બ્રોગ્લી તરંગલંબાઇમાં થતો ફેરફાર $0.50\%$ છે. ઈલેકટ્રોનનું શરૂઆતનું વેગમાન કેટલું હશે?View Solution
- 10View Solutionઆકૃતિમાં વિદ્યુત/ચુંબકીય ક્ષેત્રમાં ગતિ કરતાં ઈલેક્ટ્રોન માટે ચાર પરિસ્થિતિઓ દર્શાવેલ છે. ક્યા કિસ્સામાં ઈલેક્ટ્રોનની દી-બ્રોગ્લી તરંગલંબાઈ વધે છે ?
