નીચે બે વિધાન આપેલા છે :
વિધાન $I$ : $A+B \rightarrow C$ પ્રક્રિયા માટે વેગ નિયમ, વેગ $(r)=k[A]^2[B]$ છે. જ્યારે $A$ અને $B$ એમ બંને ની સાંદ્રતા બમણી કરવામાં આવે છે ત્યારે પ્રક્રિયા વેગ વધી ને " $x$ " ગણો થાય છે.
વિધાન $II$ :
(Image)
આકૃતિ " " $y$ " ક્રમ પ્રક્રિયા માટે સાંદ્રતામાં તફ઼ાવત સામે સમયનો આલેખ દર્શાંવે છે. $x+y$ નું મૂલ્ય . . . . . છે.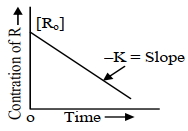
JEE MAIN 2024, Medium
Download our app for free and get started
b
$\mathrm{r}=\mathrm{K}[\mathrm{A}]^2|\mathrm{~B}|$
$\mathrm{r}=\mathrm{K}[\mathrm{A}]^2|\mathrm{~B}|$
if conc. are doubled
$\mathrm{r}^{\prime}=\mathrm{K}[2 \mathrm{~A}]^2[2 \mathrm{~B}]^1$
$\mathrm{r}^{\prime}=8 \mathrm{r} \Rightarrow \mathrm{x}=8$
(Image)
$\Rightarrow \text { Zero order, } y=0$
$x+y=8$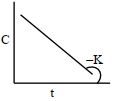
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રથમ ઓર્ડર પ્રક્રિયા માટે $A \rightarrow 2 B$માં $100$ મિનિટ પછી $1$ મોલ પ્રક્રિયક $A$ પછી $B$ ના $0.2$ મોલ્સ આપે છે. પ્રક્રિયાનું અર્ધઆયુષ્ય $.....\,min$ છે. [ઉપયોગ કરો $: \ln 2=0.69, \ln 10=2.3$View Solution
$log$નો ગુણધર્મ $\ln \left(\frac{{x}}{{y}}\right)=\ln {x}-\ln {y}$
- 2રાસાયણિક પ્રક્રિયાનો દર દરેક વધતા $10\,^oC$ તાપમાન માટે બમણો હોય છે. જો તાપમાન $50\,^oC$ સુધી વધે છે. તો પ્રક્રિયાનો દર કેટલા ગણો થશે?View Solution
- 3પ્રક્રિયા $aA \to xP$ માટે જ્યારે $[A] = 2.2\, M$ હોય ત્યારે વેગ $2.4\, m\,Ms^{-1}$ છે. $A$ ની સાંદ્રતા અડધી કરતા પ્રક્રિયાવેગ $0.6\, m\,Ms^{-1}$ થાય $A$ સંદર્ભમાં પ્રક્રિયાનો કમ જણાવો.View Solution
- 4પ્ર્કિયકની શરૂઆતની સાંદ્રતા $0.02\, M$ ધરાવતા એક શૂન્ય ક્રમની પ્રક્રિયાનો અર્ધઆયુષ્ય સમય $100\, s$ છે. તો પ્રક્રિયા માટે વેગ અચળાંક ($mol\, L ^{-1} s ^{-1}$ માં$)$ જણાવો.View Solution
- 5$n^{th } $ ક્રમની પ્રક્રિયાનો દર અચળાંક ..... એકમ ધરાવે છે.View Solution
- 6પ્રક્રિયાનો વેગ આર્હેનિયસ સમીકરણ $K=A\,e-^{E/RT}$ દ્વારા રજૂ કરવામાં આવે છે. આ સમીકરણમાં $E$ ...... છે.View Solution
- 7એક પ્રથમ ક્રમ પ્રક્રિયા એ વેગ અયળાંક $k =4.6 \times 10^{-3}\,s ^{-1}$ ધરાવે છે. નીચે આપેલામાંથી સાચાં વિધાન/નો ની સંખ્યા $.............$ છે.આપેલ: $\log 3=0.48$View Solution
$A.$ $1000\,s$ માં પ્રક્રિયા પૂર્ણ થાય છે.
$B.$ પ્રક્રિયા $500\,s$ નો અર્ધ-આયુષ્ય ધરાવે છે.
$C.$ $90 \%$ પૂર્ણ થવા માટેનો લાગતો જરૂરી સમય કરતાં $10 \%$ પૂર્ણ થવા માટે નો જરૂરી સમય $25$ ગણો છે.
$D.$ વિયોજન અંશ એ (1- $\left.e ^{-k t}\right)$ ને સમાન છે.
$E.$ વેગ (દર) અને વેગ અચળાંક (દર અચળાંક) સમાન એકમ ધરાવે છે.
- 8પ્રતિક્રિયા માટેનો અચળ દર ,$2N_2O_5 \to 4NO_2 + O_2$ $3.0\times 10^{- 4}\,s^{-1}$ છે. જો $N_2O_5$, ના $1.0\,mol\,L^{-1}$ સાથે પ્રારંભ કરો,$O_2$ ની સાંદ્રતા $0.1\, mol\, L^{-1}$. છે ત્યારે પ્રક્રિયાના ક્ષણે $NO_2$ ની રચનાની ગણતરી કરો.View Solution
- 9પ્રથમ ક્રમ પ્રક્રિયામાં $a/(a - x) 10$ મિનિટ પછી $8$ મળે છે તો દર અચળાંક શું થશે?View Solution
- 10ચાર જુદી જુદી પ્રક્રિયાઓ માટે વેગ અચળાંક વિરુદ્ધ $\frac{1}{\mathrm{T}}$ ના નીચેના આલેખ ધ્યાનમાં લો. તો આ પ્રક્રિયાઓની સક્રિયકરણ ઊર્જાઓ માટે નીચેના પૈકી ક્યો ક્રમ સાચો છે ?View Solution
