પાતળા સળિયાના કેન્દ્રમાંથી પસાર થતી અને લંબાઈ $ ℓ$ ને લંબ અક્ષ પર જડત્વની ચાકમાત્રા $ I $ છે. આવા ચાર સળિયાના ચોરસના કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?
Medium
d
\(\begin{gathered}
\,I\,\, = \,\,\frac{{m{L^2}}}{{12}}\,\,\,\,\,\therefore \,\,I'\,\, = \,\,4\,\,\left[ {\frac{{m{L^2}}}{{12}}\,\, + \;\,\frac{{m{L^2}}}{4}} \right] \hfill \\
I'\,\, = \,\,4\,\,\left[ {\frac{{m{L^2}}}{3}} \right]\,\, = \,\,\frac{4}{3}\,\,M{L^2}\,\,\,\therefore \,\,m{L^2}\,\, = \,\,12I \hfill \\
I'\,\, = \,\,\frac{4}{3}\,\, \times \,\,12I\,\, = \,\,16I \hfill \\
\end{gathered} \)
\(\begin{gathered}
\,I\,\, = \,\,\frac{{m{L^2}}}{{12}}\,\,\,\,\,\therefore \,\,I'\,\, = \,\,4\,\,\left[ {\frac{{m{L^2}}}{{12}}\,\, + \;\,\frac{{m{L^2}}}{4}} \right] \hfill \\
I'\,\, = \,\,4\,\,\left[ {\frac{{m{L^2}}}{3}} \right]\,\, = \,\,\frac{4}{3}\,\,M{L^2}\,\,\,\therefore \,\,m{L^2}\,\, = \,\,12I \hfill \\
I'\,\, = \,\,\frac{4}{3}\,\, \times \,\,12I\,\, = \,\,16I \hfill \\
\end{gathered} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1તકતીના કેન્દ્ર પર એક છોકરો હાથમાંં બે બ્લોક લઈને ઊભો છે. તે કેન્દ્રમાંથી પસાર થતી લંચ અક્ષ પર તંત્રની ગતિ ઊર્જા $K$ છે. જ્યારે છોકરો તેના હાથ ખુલ્લા કરે ત્યારે તંત્રની ભ્રમણ અક્ષ પર જડત્વની ચાકમાત્રા બમણી થઈ જાય છે. તો તંત્રની નવી ગતિ ઊર્જા કેટલી થશે ?View Solution
- 2એક મોટરસાઇકલ રોડ પર $ 54\;kmh^{-1}$ ની ઝડપથી ગતિ કરે છે. તેના પૈડાઓની ત્રિજયા $0.45\;m$ અને તેના ભ્રમણ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $3 \;kgm^2$ છે. જો આ વાહન $15$ સેકન્ડમાં સ્થિર થાય, તો બ્રેક દ્વારા પૈડા પર લાગતા સરેરાશ ટોર્કનું મૂલ્ય ($kg\,m^2\,s^{-2}$ માં) કેટલું હશે?View Solution
- 3$m$ દળનો એક વિસ્ફોટ કણ જમીનથી અમુક ઊચાઈએ આવેલા $ [x - y]$ સમક્ષિતિજ સમતલમાં $x - $ અક્ષ સાથે ગતિ કરે છે. જો તે અચાનક ફૂટીને $ m/4 $ અને $3m/4$ દળ ધરાવતા કણોમાં વહેચાય છે. તે ક્ષણ પછી નાનો કણ $y = 15\ cm$ સ્થાને હોય છે. આ ક્ષણે મોટો કણ $y =$ ........ $cm$ સ્થાન હશે .View Solution
- 4એક રમતના મેદાનમાં એક ગોળ ફરતી તકતી જેનું વજન $120\ kg$ ત્રિજ્યા $4\ m$ અને ચક્રમાન ત્રિજ્યા $3\ m$ છે જ્યારે તકતી સ્થિર હોય ત્યારે એક $30\ kg$ દળનું બાળક $5\ m/sec$ ના વેગથી ટકટીના સ્પર્શકની દિશામાં તકતી પર ચડે છે જો ઘર્ષણને અવગણવામાં આવે તો બાળક અને ટકતીનો કોણીય વેગ ......... $ rad/sec$ થાય .View Solution
- 5$R$ ત્રિજયા અને $R\over 6 $ જાડાઇ ઘરાવતી તકતીની જડત્વની ચાકમાત્રા $I$ છે. તેને પીગળાવીને ગોળો બનાવવામાં આવે તો ગોળાની જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
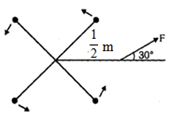
- 6$2\ kg$ ના દળોને $1/4\ m $ લાંબા સ્પોક્સ વડે ધરી સાથે આકૃતિ $A$ માં દર્શાવ્યા પ્રમાણે જોડેલા છે. $24\ N$ નું બળ $ F$ એ $1/2\ m$ લાંબા હાથના છેડે લગાવતા કોણીય પ્રવેગ $\alpha$ પેદા થાય છે. $\alpha$ નું મૂલ્ય ........ $ rad/s^2$View Solution
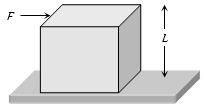
- 7$L$ લંબાઇનો સમઘન બ્લોક $\mu $ ઘર્ષણાક ધરાવતી સપાટી પર પડેલો છે આકૃતિમાં દર્શાવ્યા મુજબ એક બળ $F$ લગાવવામાં આવે છે. જો ઘર્ષણાક નું મૂલ્ય એટલું ઊંચું હોય કે જેથી બ્લોક ખ્સયા પહેલા ઢળી પડે તો તેના માટે ન્યૂનતમ $F$ નું મૂલ્ય કેટલું હોવું જોઈએ ?View Solution
- 8View Solutionસમાન ત્રિજ્યાના એક નક્કર ગોળો અને તકતી ઢોળાવવાળી સપાટી પર લપસ્યા વગર પડે છે. એક એ બીજા કરતા વહેલા પહોંચે છે તેનું કારણ
- 9એક અવગણ્ય દળની સ્પ્રિંગ વડે જોડેલા $5 \,kg$ અને $2 \,kg$ દળનાં બે બ્લોકને એક ઘર્ષણરહિત સમક્ષિતિજ સપાટી પર રાખવામાં આવ્યા છે. જો ભારે બ્લોકને ધક્કો (Impulse) લગાવતાં તેને હળવા બ્લોકની દિશામાં $7 \,m / s$ નો વેગ પ્રાપ્ત કરે છે. દ્રવ્યમાન કેન્દ્રનો વેગ .......... $m / s$ થાય.View Solution
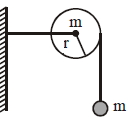
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે $\mathrm{m}$ દળને એક દળરહિત દોરી વડે બાંધી એક $\mathrm{r}$ ત્રિજ્યા અને $m$ દળની તકતી સાથે લટકાવેલ છે.જ્યારે તેને મુક્ત કરાવમાં આવે છે ત્યારે તે નીચે તરફ ગતિ કરવાનું શરૂ કરે છે. જ્યારે તે નીચે $h$ અંતર કાપે ત્યારે તકતીની કોણીય ઝડપ કેટલી hશે?View Solution