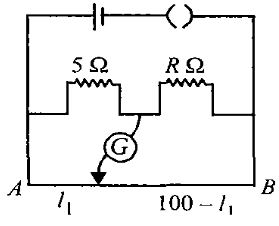
પરિપથના $P$ અને $Q$ બિંદુ વચ્ચે સમતુલ્ય અવરોધ ......

AIIMS 2013, Medium
a
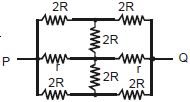
The circuit is symmetrical about axis \(POQ\). Therefore the equivalent circuit is drawn
The circuit is symmetrical about axis \(POQ\). Therefore the equivalent circuit is drawn
\(\therefore \) \(\frac{1}{\mathrm{R}_{\mathrm{PQ}}}=\frac{1}{4 \mathrm{R}}+\frac{1}{4 \mathrm{R}}+\frac{1}{2 \mathrm{r}}\) \(=\frac{1}{2 \mathrm{R}}+\frac{1}{2 \mathrm{r}}\) \(=\frac{\mathrm{R}+\mathrm{r}}{2 \mathrm{Rr}}\)
\(\Rightarrow \mathrm{R}_{\mathrm{PQ}}=\frac{2 \mathrm{Rr}}{\mathrm{R}+\mathrm{r}}\)
If a potential difference is applied across \(P\) and \(Q,\) there will be no currents in arms \(AO\) and \(OB\). So these resistance will be ineffective.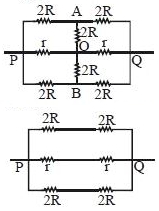
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કોષને $ 2\,Ω$ અવરોધ સાથે જોડતાં $0.5\, A $ અને $ 5\,Ω $ સાથે જોડતાં $0.25 \,A$ પ્રવાહ પસાર થાય છે,તો કોષનો $ emf$ કેટલા .............. $volt$ થાય?View Solution
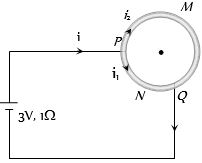
- 2$10\, \Omega$ અવરોધ ધરાવતા વાયરને વર્તૂળાકારે વાળેલ છે. $P$ અને $Q$ વર્તૂળની પરીઘ પરના બે બિંદુઓ છે જે વર્તૂળને ચતુર્થ ભાગમાં વિભાજીત કરે છે તથા આ બે બિંદુઓને $3\,V$ તથા $1\, \Omega$ આંતરીક અવરોધ ધરાવતી બેટરી સાથે જોડતા વર્તૂળના બંને ભાગોમાંથી પસાર થતા પ્રવાહો.... હશે.View Solution
- 3$12$ $V$ અને $13$ $V$ $emf$ ધરાવતી બે બેટરીઓને $10$ $Ω$ ભાર અવરોધ સાથે સમાંતરમાં જોડેલ છે.બંને બેટરીઓના આંતરિક અવરોધ અનુક્રમે $1$ $\Omega$ અને $2$ $\Omega$ છે.ભાર અવરોધને સમાંતર વોલ્ટેજ _______ ની વચ્ચે હશે.View Solution
- 4સમાન વ્યાસ ધરાવતા ચાર તારને સમાન વિદ્યુતસ્થિતિમાન પર લગાવવામાં આવે છે.તેમની અવરોધકતા અને લંબાઈ $\rho$ અને $L$ (તાર $1$) $1.2\,\rho$ અને $1.2\,L$ (તાર $2$ ), $0.9\,\rho $ અને $0.9\,L$ (તાર $3$ ) અને $\rho$ અને $1.5\,L$ (તાર $4$ ). તો ઉત્પન્ન થતી ઉષ્મા ઉતરતા ક્રમમાં ગોઠવો.View Solution
- 5‘ $l$ ' લંબાઈના અને $100 \Omega$ અવરોધ ધરાવતા એક તારને $10$ સમાન ભાગોમાં વહેંચવામાં આવે છે. પ્રથમ $5$ ભાગોને શ્રેણીમાં જ્યારે બાકીના $5$ ભાગોને સમાંતરમાં જોડવામાં આવે છે. આ બંને સંયોજનોને ફરી વાર શ્રેણીમાં જોડવામાં આવે છે. અંતિમ સંયોજનનો અવરોધ. . . . . . . . . થશે.View Solution
- 6View Solutionજે જુદી જુદી ધાતુના જંકશનમાંથી વિધુત પ્રવાહ પસાર કરતા જંકશન આગળ ઉત્સર્જાતી અથવા શોષાતિ ઉષ્માને કયા નિયમથી ઓળખાય છે ?
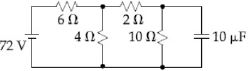
- 7આપેલ પરિપથમાં કેપેસીટર પર કેટલા ............... $\mu C$ વિજભાર હશે?View Solution
- 8$0\,^oC$ તાપમાને પ્લેટીનીયમ અવરોધ થર્મોમીટરમાં કોઈલનો અવરોધ $5$ ઓહમ છે $100\,^oC$ અને તાપમાને $5.75$ ઓહમ છે. અજ્ઞાત તાપમાને તેનો અવરોધ $5.15 $ ઓહમ છે. તો અજ્ઞાત તાપમાન ............ $^oC$ હશે.View Solution
- 9બે અવરોધો $r_1$ અને. $r_2$ ને સમાંતરમાં જોડેલા છે. $\left(r_1 < r_2\right)$ તો સમતુલ્ય અવરોધ $R$એ કેવી રીતે હશે?.View Solution
- 10મીટરબ્રીજની બે ભુજાઓના અવરોધો અનુક્રમે $5\,\Omega$ અને $R\,\Omega$ છે. જયારે અવરોધ $R $ ની સાથે સમાન અવરોધનો શંટ જોડતાં નવો બેલેન્સ પોઇન્ટ $1.6 l_1 $ મળે છે. અવરોધ $R=$ .................. $\Omega$View Solution