$PV^n$ અચળ સમીકરણ મુજબ આદર્શવાયુ ઉષ્મીય પ્રક્રિયા કરે છે. આ પ્રક્રિયા દરમિયાન મોલર વિશિષ્ટ ઉષ્માક્ષમતા અચળ ક્દે અને અચળ દબાણે મોલર વિશિષ્ટ ઉષ્માક્ષમતાની સરેરાશ જેટલી હોય તો $n$ નું મૂલ્ય કેટલું હશે?
Diffcult
Download our app for free and get started
b
(b)
(b)
Polytropic process
\(P V^m=\) constant
Given heat capacities is average of \(C_P\) and \(C_V\) So
\(C=\frac{C_P+C_V}{2}\)
or \(\quad C=\frac{2 C_V+R}{2}\)
or \(\quad C=\frac{C_V+R}{2} \quad \dots (i)\)
Now formula for specific heat of polytropic process is given by
\(C=\frac{R}{y-1}+\frac{R}{1-n} \quad \dots (ii)\)
or \(\frac{R}{y-1}+\frac{R}{2}=\frac{R}{y-1}+\frac{R}{1-n}\) as \(C_V=\frac{R}{y-1}\)
\(\frac{R}{2}=\frac{R}{1-n}\)
or \(n=-1\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક ઉષ્મીય રીતે અલગ પાડેલ રૂમમાં ફ્રિજનો દરવાજો ખુલ્લો રાખતા રૂમમાં રહેલ હવાનું તાપમાન...
- 2એક દ્વિપરમાણ્વિક વાયુ $P V^{1.3}=$ અચળ વડે રજૂ કરેલ પ્રક્રિયામાંથી પસાર થાય છે. સાચુ નિવેદન પસંદ કરો.View Solution
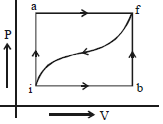
- 3જ્યારે એક તંત્રને આકૃતિમાં દર્શાવ્યા મુજબ $i$ અવસ્થામાંથી $f$ અવસ્થામાં $iaf$ માર્ગ દ્વારા લઈView Solution
માર્ગથી લઈ જવામાં આવે ત્યારે $Q = 50\, cal$ અને $W = 20\, cal$ મળે અને $ibf$ માર્ગ પર $Q = 36\, cal.$ છે
$(i)$ $ibf$ માર્ગ પર કાર્ય $W$ કેટલું હશે?
$(ii)$ જો $fi$ માર્ગ પર $W = 13\;cal$ હોય તો આ માર્ગ પર $Q$ કેટલો હશે?
$(iii)$ જો $E_{int,i} = 10\,\, cal$ હોય તો $E_{int,f}$ કેટલો હશે?
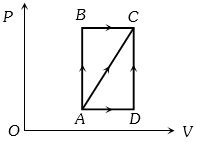
- 4આકૃતિમાં એક થરમોડાઇનેમિક પ્રક્રિયા દર્શાવેલ છે.આકૃતિમાં દર્શાવેલ બિંદુઓએ દબાણ અને કદ આ મુજબ છે.View Solution
${P_A} = 3 \times {10^4}\;Pa,\;{P_B} = 8 \times {10^4}\;Pa$ અને ${V_A} = 2 \times {10^{ - 3}}\;{m^3},\;{V_D} = 5 \times {10^{ - 3}}\;{m^3}$
$AB$ પ્રક્રિયામાં તંત્રમાં $600\;J$ ઉષ્મા ઉમેરવામાં આવે છે અને $BC$ પ્રક્રિયામાં $200\;J$ ઉષ્મા ઉમેરવામાં આવે છે. $AC$ પ્રક્રિયા દરમિયાન થતો આંતરિક ઊર્જાનો ફેરફાર ..... $J$ હશે.
- 5એક તળાવમાં $h$ ઊંડાઈથી માછલી દ્વારા $Vo$ કદનો પરપોટો છોડવામાં આવે છે. પરપોટો સપાટી પર આવે છે. અચળ તાપમાન અને પ્રમાણભૂત વાતાવરણ દબાણ ધારો સપાટી પર, તો પરપોટો જ્યારે સપાટી પર પહોચે તેની પહેલા તેનું કદ, પાણીની ઘનતા $\rho$View Solution
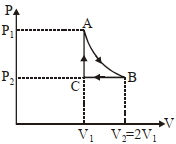
- 6$n$ મોલ ધરાવતાં એક આદર્શવાયું ચક્રિય પ્રક્રિયા $ABCA$ માંથી પસાર થાય છે. (આકૃતિ જુઓ), કે જે નીચેની પ્રક્રિયાઓ ધરાવે છે.View Solution
$A \rightarrow B$ : $T$ તાપમાને સમતાપીય વિસ્તરણકે જેમાં કદ $V _{1}$ થી $V _{2}=2 V _{1}$ બમણું થાય છે અને દબાણ બદલાઈને $P _{1}$ થી $P _{2}$ થાય છે.
$B \rightarrow C$ ; અચળ દબાણ $P _{2}$ એ સમદાબીય સંકોચન દ્વારા પ્રારંભિક કદ $V _{1}$
$C \rightarrow A$ : અચળ કદે કે જે દબાણમાં $P _{2}$ થી $P _{1}$ ફેરફાર કરે છે.
એક પૂર્ણ ચક્રિય પ્રક્રિયા ABCA દરમ્યાન થતું કુલ કાર્ય ,......... થશે.
- 7View Solutionનીચેનામાથી કઈ થર્મોડાયનેમિક પ્રક્રિયામાં તંત્રની એન્ટ્રોપી બદલાય નહીં.
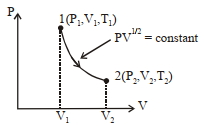
- 8$1$ મોલ આદર્શ વાયુ માટે, ઉષ્માગતિશાસ્ત્ર પ્રક્રિયાને $P-V$ આકૃતિ દ્વારા દર્શાવવામાં આવેલ છે. જે $V _{2}=2 V _{1}$ હોય તો તાપમાનનો ગુણોત્તર $T _{2} / T _{1}$ ........ છે.View Solution
- 9જો કાર્નોટ એન્જિન ઉષ્મા પ્રાપ્તિ તાપમાન $127^{\circ} C$ અને ઠારણ વ્યવસ્થા તાપમાન $87^{\circ} C$ ની વચ્ચે કાર્ય કરે છે, તો તેની કાર્યક્ષમતા ........ $\%$ છે ?View Solution
- 10એક બલૂનમાં $\left(32^{\circ} C \right.$ તાપમાને અને $1.7\;atm$ તાપમાને હીલિયમ વાયુ ભરેલ છે. જ્યારે બલૂન તૂટે ત્યારે તરત જ હીલિયમ વાયુનું વિસ્તરણ કેવું ગણી શકાય?View Solution