Speed of wind on the upper surface of the wing, \(V_{1}=70 m / s\) Speed of wind on the lower surface of the wing, \(V_{2}=63 m / s\) Area of the wing, \(A=2.5 m ^{2}\) Density of air, \(\rho=1.3 kg m ^{-3}\)
According to Bernoulli's theorem, we have the relation:
\(P_{1}+\frac{1}{2} \rho V_{1}^{2}=P_{2}+\frac{1}{2} \rho V_{2}^{2}\)
\(P_{2}-P_{1}=\frac{1}{2} \rho\left(V_{1}^{2}-V_{2}^{2}\right)\)
Where,
\(P_{1}=\) Pressure on the upper surface of the wing
\(P_{2}=\) Pressure on the lower surface of the wing
The pressure difference between the upper and lower surfaces of the wing provides lift to the aeroplane.
Lift on the wing \(=\left(P_{2}-P_{1}\right) A\)
\(=\frac{1}{2} \rho\left(V_{1}^{2}-V_{2}^{2}\right) A\)
\(=\frac{1}{2} 1.3\left((70)^{2}-(63)^{2}\right) \times 2.5\)
\(=1512.87\)
\(=1.51 \times 10^{3} N\)
Therefore, the lift on the wing of the aeroplane is \(1.51 \times 10^{3} \;N\).
Download our appand get started for free
Similar Questions
- 1$5\, cm$ ત્રિજ્યા ધરાવતી પાઇપમાથી પાણી $100\,$ લિટર પ્રતિ મિનિટ ના દરથી આવે તો પ્રવાહનો રેનોલ્ડ નંબર કયા ક્રમનો હશે? (પાણીની ઘનતા $= 1000\, kg/m^3$, પાણીનો શ્યાનતાગુણાંક $= 1\, mPa\, s$)View Solution
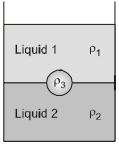
- 2એક બરણીમાં, એકબીજામાં મિશ્રિત ન થઇ શકે તેવાં તથા $\rho_{1}$ અને $\rho_{2}$ ધનતાવાંં બે પ્રવાહી ભરેલાં છે. આ બરણીમાં $\rho_{3}$ ધનતાવાળો ગોળો નાખતા તે આકૃતિમાં દર્શાવ્યા મુજબની સંતુલન સ્થિતિ પ્રાપ્ત કરે છે. તો નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.View Solution
- 3સમક્ષિતિજ રાખેલ પાઇપમાં કેરોસીનનો વેગ $ 5 m/s$ છે.તો વેલોસીટી હેડ ...... $m$ થાય?($g = 10m/{s^2}$ )View Solution
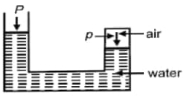
- 4મર્યાદિત હવાનું દબાણ $p$ છે. જો વાતાવરણનું દબાણ $P$ છે તો...View Solution
- 5$\rho$ ઘનતાના પ્રવાહીને સમાવતું બીકર એ પ્રવેગ $a$ સાથે ઉપર ગતિ કરે છે. પ્રવાહીની સપાટીથી $h$ ઊંંડાઈએ પ્રવાહીને લીધે લાગતું દબાણ કેટલું છે ?View Solution
- 6નીચે બે વિધાનો આપેલા છે. એકને કથન $A$ અને બીજાને કારણ $R$ થી દર્શાવવામાં આવ્યા છે.View Solution
ક્થન $(A)$ : જ્યારે તમે ટૂથપેસ્ટને બીજા છેડેથી બહાર કાઢવા માટે ટ્યુબના એક છેડાને દબાવો છો, ત્યારે પાસ્કલનો સિદ્ધાંત જોવા મળે છે.
કારણ $(R)$ : બંધ અદબનીય પ્રવાહી પર લાગુ પાડેલ દબાણમાં ફેરફાર પ્રવાહીના દરેક ભાગ અને તેના પાત્રની દિવાલો પર ઘટ્યા વગર પ્રસારિત થાય છે.
ઉપરોક્ત વિધાનોમાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી સાચો વિકલ્પ પસંદ કરો.
- 7View Solutionવિધાન : પ્રવાહમાં જ્યારે દબાણ વધુ હોય ત્યાં વેગ ઓછો હોય અને ઊલટું પણ (દબાણ ઓછું અને વેગ વધુ)
કારણ : બર્નુલીના નિયમ મુજબ આદર્શ પ્રવાહીના વહન માટે એકમ દળમાં રહેલ કુલ ઉર્જા અચળ હોય.
- 8બે એકસમાન નળાકાર પાત્રને જમીન પર મૂકેલા છે જેમાં સમાન ઘનતા $d$ ધરાવતું પ્રવાહી ભરેલ છે. બને પાત્રના તળિયાનું ક્ષેત્રફળ $S$ છે પરંતુ એક પાત્રમાં પ્રવાહીની ઊંચાઈ $x_{1}$ અને બીજા પાત્રમાં પ્રવાહીની ઊંચાઈ $x_{2}$ છે. જ્યારે બંને નળાકારને નહિવત કદ ધરાવતી નળી દ્વારા પાત્રના તળીએથી જોડવામાં આવે છે જેથી જ્યાં સુધી બંને પાત્રમાં પ્રવાહી એક નવી ઊંચાઈના સંતુલનમાં ના આવે ત્યાં સુધી પ્રવાહી એક પાત્રમાંથી બીજા પાત્રમાં વહન કરે છે. આ પ્રક્રિયા દરમિયાન તંત્રની ઊર્જામાં કેટલો ફેરફાર થાય?View Solution
- 9એક લાકડાનો બ્લોક તેનું $\frac{4}{5} th$ ભાગનું કદ પાણીમાં ડૂબાયેલું રહે તેમ તરી રહ્યું છે, પરંતુ તે માત્ર બીજા પ્રવાહીમાં તરે છે. પ્રવાહીની ઘનતા કેટલી છે ? (in $kg / m ^3$ )View Solution
- 10પાત્રના તળિયે સમાન લંબાઇ ધરાવતી $r_1$ અને $ r_2$ ત્રિજયાવાળી કેશનળી જોડેલ છે.તો કેટલી ત્રિજયાની કેશનળી જોડવાથી પ્રવાહ અચળ રહે?View Solution
