Download App
રાસાયણિક પ્રક્રિયાને ધ્યાનમાં લેતાં : $N_2(g) + 3H_2(g) \rightarrow  2NH_3(g)$  આ પ્રક્રિયાનો દર તેના $N_2(g), H_2(g)$  અથવા $NH_3(g) $ ની સાંદ્રતાના સમયના સંદર્ભના સમજાવી શકાય છે તો આ દર સમીકરણ વચ્ચેનો સાચો સંબંધ શોધો.
  • A દર $\, = \,\, - \frac{{d[{N_2}]}}{{dt}}\,\, = \,\,{\text{ - }}\frac{{\text{1}}}{{\text{3}}}\,\frac{{{\text{d[}}{{\text{H}}_{\text{2}}}{\text{]}}}}{{{\text{dt}}}}\,\, = \,\,\frac{{\text{1}}}{{\text{2}}}\,\frac{{{\text{d[N}}{{\text{H}}_{\text{3}}}{\text{]}}}}{{{\text{dt}}}}{\text{ }}$
  • B દર $\, = \, - \frac{{d[{N_2}]}}{{dt}}\,\, = \,\, - \frac{{3d[{H_2}]}}{{dt}}\,\, = \,\,\frac{{2d[N{H_3}]}}{{dt}}$
  • C દર $\,\, = \,\,\frac{{d[{N_2}]}}{{dt}}\,\, = \,\,\frac{1}{3}\,\frac{{d[{H_2}]}}{{dt}}\,\, = \,\,\frac{1}{2}\,\frac{{d[N{H_2}]}}{{dt}}$
  • D દર $\, = \,\, - \frac{{d[{N_2}]}}{{dt}}\,\, = \, - \,\frac{{d[{H_2}]}}{{dt}}\,\, = \,\,\frac{{d[N{H_3}]}}{{dt}}$
Medium
Download our app for free and get startedPlay store
a
art

Download our app
and get started for free

Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Download App

Similar Questions

  • 1
    $2FeCl_3 + SnCl_2 \rightarrow 2FeCl_2 + SnCl_4 $ આપેલ પ્રક્રિયા ....... નું ઉદાહરણ છે.
    View Solution
  • 2
    ચોક્કસ પ્રથમ ક્રમની પ્રક્રિયા માટે $570 \,s$ પછી $32 \%$ પ્રક્રિયક બાકી રહે છે. આ પ્રક્રિયાનો વેગ અચળાંક  ...........  $\times 10^{-3} s ^{-1}$ છે.

    $\left[\right.$ આપેલ છે $\left.: \log _{10} 2=0.301, \ln 10=2.303\right]$

    View Solution
  • 3
    ${PCl}_{5}(g) \rightarrow {PCl}_{3}({~g})+{Cl}_{2}({~g})$

    ઉપરોક્ત પ્રથમ ક્રમની પ્રક્રિયામાં $300\, {~K}$ પર $120$ મિનિટમાં ${PCl}_{5}$ની સાંદ્રતા પ્રારંભિક સાંદ્રતા $50\, mol\,{L}^{-1}$ થી $10\, {~mol} \,{~L}^{-1}$ થી ઘટે છે. $300\, {~K}$ પર પ્રક્રિયા માટે દર અચળાંક ${X}$ $\times 10^{-2} \,{~min}^{-1}$ છે. $x$ ની કિંમત $......$ છે.

    $[$ આપેલ છે: $\log 5=0.6989]$

    View Solution
  • 4
    $N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)}$  પ્રક્રિયા તાપમાનની ચોક્કસ પરિસ્થિતિ અને પ્રક્રિયકોનું આંશિક દબાણ હેઠળ થાય છે.  $ NH_3$ નો નિર્માણ દર $ 0.001\,\,kg\, h^{-1}$ છે. તો $H_2$ નો રૂપાંતરણ દર તેજ સમાન પરિસ્થિતિમાં......$kg \,h^{-1}$ છે.
    View Solution
  • 5
    ચોક્કસ ઉત્સેચક-ઉત્પ્રેરિત પ્રક્રિયામાં પદાર્થનું અર્ધ આયુષ્ય સમય $138\, s$  છે , પદાર્થની સાંદ્રતા માટે જરૂરી સમય  $1.28\, mg \,L^{-1}$  થી $0.04\, mg\, L^{-1}$ ....... $\sec$ શું થશે 
    View Solution
  • 6
    પ્રથમ ક્રમ પ્રક્રિયાનો અદ્ય આયુ સમય $10$  મિનિટ છે. જો પ્રારંભિક મૂલ્ય $0.08$ મોલ/લીટર અને કોઈ  જ ક્ષણે તેની સાંદ્રતા $0.01$ મોલ/લીટર હોય તો ...... મિનિટ થાય.
    View Solution
  • 7
    જ્યારે તાપમાનનો ફેરફાર $20\,^oC$ થી $50^o$ થાય તો પ્રક્રિયાનો દર ત્રણ ગણો થાય. તો પ્રક્રિયા માટેની સક્રિયકરણ ઊર્જા $=$ …. $ KJ \,mol^{-1} $ ($R = 8.314 \,JK^{-1} $ મોલ $^{-1} $)
    View Solution
  • 8
    નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.

    $\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$

    પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.

    સ્ટેપ

    Rate constant $\left(\sec ^{-1}\right)$

    Activation energy 

    $\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
    $1$ ${k}_1$ $300$
    $2$ ${k}_2$ $200$
    $3$ ${k}_3$ $\mathrm{Ea}_3$

    ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).

    View Solution
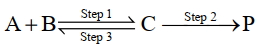
  • 9
    એક પ્રથમ ક્રમની પ્રક્રિયાના $99.9\%$ પૂર્ણ થવા માટેનો જરૂરી સમય એ પ્રક્રિયાના અર્ધ આયુષ્ય $\left(\mathrm{t}_{1 / 2}\right)$ ના____________ સમય જેટલો છે.
    View Solution
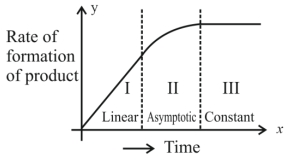
  • 10
    એક નિશ્ચિત રાસાયણિક પ્રક્રિયા $X \rightarrow Y$ માટે, નીપજના બનવાનો દર વિરુદ્ધ સમયનો ગ્રાફ (આલેખ) એ આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચાં વિધાન/નોની સંખ્યા $..............$ છે.

    $(A)$ સમગ્ર પ્રક્રિયાનો ક્રમ છે.

    $(B)$ આ પ્રક્રિયાનો ક્રમ શોધી શકાતો નથી.

    $(C)$ $I$ અને $III$ વિભાગ માં, પ્રક્રિયા અનુક્રમે પ્રથમ અને શૂન્ય ક્રમની છે.

    $(D)$ વિભાગ $II$ માં, પ્રક્રિયા પ્રથમક્રમની છે.

    $(E)$ વિભાગ $II$ માં, પ્રક્રિયાનો ક્રમ $0.1$ થી $0.9$ વિસ્તાર માં છે.

    View Solution