શિરોલંબ સમતલમાં એક પાતળી નળીને વાળીને $r$ ત્રિજ્યાનું વર્તુળ બનાવવામાં આવે છે.${\rho _1}$ અને ${\rho _2}\left( {{\rho _1} > {\rho _2}} \right)$ ઘનતા ધરાવતા બે સમાન કદબા એકબીજામાં મિશ્ર ના થાય તેવા પ્રવાહી દ્વારા અડધું વર્તુળ ભરેલ છે.શિરોલંબ અને બંને પ્રવાહી મળતા હોય તે સપાટી વચ્ચે વચ્ચેનો ખૂણો $\theta$ કેટલો થાય?
JEE MAIN 2018, Diffcult
a
Pressure at interface \(A\) must be same from both the sides to be in equilibrium.
Pressure at interface \(A\) must be same from both the sides to be in equilibrium.
\(\therefore \left( {R\cos \theta + R\sin \theta } \right){\rho _2}g\)
\( = \left( {R\cos \theta - R\sin \theta } \right){\rho _1}g\)
\( \Rightarrow \frac{{{\rho _1}}}{{{\rho _2}}} = \frac{{\cos \theta + \sin \theta }}{{\cos \theta - \sin \theta }} = \frac{{1 + \tan \theta }}{{1 - \tan \theta }}\)
\( \Rightarrow {\rho _1} - {\rho _1}\,\tan \,\theta = {\rho _2} + {\rho _2}\,\tan \,\theta \)
\( \Rightarrow \left( {{\rho _1} + {\rho _2}} \right)\tan \theta = {\rho _1} - {\rho _2}\)
\(\therefore \theta = {\tan ^{ - 1}}\left( {\frac{{{\rho _1} - {\rho _2}}}{{{\rho _1} + {\rho _2}}}} \right),so\,closest\,answer\,is\left( a \right)\)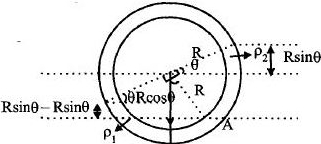
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક હાઈડ્રોલીક પ્રેસ $100\, kg$ ને ઊંચકી શકે છે જ્યારે $‘m'$ જેટલું દળ નાના પિસ્ટન પર મૂકવામાં આવે છે. દળ ને $‘m’$ જેટલું સમાન રાખીને જો મોટા પીસ્ટનનો વ્યાસ $4$ ગણો વધારવામાં આવે અને નાના પીસ્ટનનો વ્યાસ $4$ ગણો ઘટાડવામાં આવે તો તે ............... $kg$ દળ ઊંચકી શકશે.View Solution
- 2મોટી ટાંકીના આડછેદનું ક્ષેત્ર $0.5 \,m ^{2}$ છે. તેને તળિયા આગળ $1 \,cm ^{2}$ જેટલું આડછેદનું ક્ષેત્રફળ ધરાવતું નાનું છિદ્ર છે. ટાંકીમાં પાણીની ઉપર $25 \,kg$ નો ભાર લગાડવામાં આવે છે. ટાંકીમાં પાણીની ઝડપ અવગણી ટાંકીના તળિયાથી પાણીની ઉંચાઈ $40 \,cm$ હોય ત્યારે છિદ્રમાંથી બહાર આવતાં પાણીનો વેગ ............. $cms ^{-1}$ હશે. $\left[ g =10 \,ms ^{-2}\right.$ લો.]View Solution
- 3View Solutionપ્રવાહીમાં પદાર્થ તરે છે,પાત્રને મુકત પતન કરાવતાં પ્રવાહી દ્વારા લાગતું ઉત્પલાવક બળ કેટલું થાય ?
- 4$20\; m$ ની ઊંચાઈનો નળાકાર સંપૂર્ણપણે પાણીથી ભરેલો છે. તેના તળિયાની નજીક નળાકારની બાજુની દિવાલ પરના નાના છિદ્રમાંથી બહાર આવતા પાણીના પ્રવાહનો વેગ ($ m/s$ માં) કેટલો હશે?View Solution
- 5$L $ અને $ 2L $ લંબાઇ અને $ R$ અને $2R $ ત્રિજયાની કેશનળીને શ્રેણીમાં જોડેલ છે.તો દર સેકન્ડે બહાર આવતાં પ્રવાહીનું કદ કેટલું હોય? (પ્રથમ નળીમાંથી બહાર આવતાં પ્રવાહીનું કદ $X = \pi P{R^4}/8\eta L$)View Solution
- 6પાણીની ટાંકીના તળિયા થી એક પત્થર ને ઉપર તરફ શિરોલંબ દિશામાં પ્રક્ષેપિત કરવામાં આવે છે. પાણીના અવરોધને અવગણતા તે ઉપર તરફ અને નીચે તરફ સરખા સમયમાં જાય છે પરંતુ જો પાણીના ખેચાણની હાજરીમાં તેને ઉપર તરફ જતાં લાગતો સમય $t_{up}$ અને નીચે તરફ જતાં લાગતો સમય $t_{down}$ હોય તો તે બંને વચ્ચેનો સંબંધ શું થાય?View Solution
- 7પવનની ટનલમાં એક નમૂના (model)ના વિમાન પરના પ્રયોગમાં પાંખની ઉપર અને નીચેની સપાટીઓ આગળ વહનની ઝડપ અનુક્રમે $70\, m\,s^{-1}$ અને $63\, m\, s^{-1}$ છે. જો પાંખનું ક્ષેત્રફળ $2.5\, m^2$ હોય તો પાંખ પર ઊર્ધ્વ ધક્કો (બળ) (lift) કેટલો હશે ? હવાની ઘનતા $1.3\, kg\, m^{-3}$ લો .View Solution
- 8એક હાઈડ્રોલીક પ્રેસ $100\, kg$ ને ઊંચકી શકે છે જ્યારે $‘m'$ જેટલું દળ નાના પિસ્ટન પર મૂકવામાં આવે છે. દળ ને $‘m’$ જેટલું સમાન રાખીને જો મોટા પીસ્ટનનો વ્યાસ $4$ ગણો વધારવામાં આવે અને નાના પીસ્ટનનો વ્યાસ $4$ ગણો ઘટાડવામાં આવે તો તે ............... $kg$ દળ ઊંચકી શકશે.View Solution
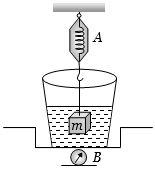
- 9એક સ્પ્રિંગકાંટો $A$ તેની સાથે લટકાવેલ બ્લોક $m$ નું અવલોકન $2\, kg$ દર્શાવે છે. જ્યારે વજનકાંટા $B$ પર મૂકેલું બીકર પ્રવાહીથી ભરવામાં આવે છે ત્યારે તે $5 \,kg $ અવલોકન દર્શાવે છે. આકૃતિ માં દર્શાવ્યા મુજબ લટકાવેલું દળ પ્રવાહીની અંદર રહે તેમ બંને વજનકાંટા ને ગોઠવેલા છે. આ પરિસ્થિતી માં .....View Solution
- 10$16 \,cm ^{2}$ જેટલું સમાન આડછેદનું ક્ષેત્રફળ ધરાવતા બે નળાકારીય વાસણો (પાત્રો)માં અનુક્રમે $100 \,cm$ અને $150 \,cm$ ઊંચાઈ સુધી પાણી ભરવામાં આવેલ છે. આ પાત્રોને જોડવામાં આવે છે કે જેથી તેઓમાં પાણીનું સ્તર સમાન ઊંચાઈએ થાય. આ પ્રક્રિયા દરમિયાન ગુરુત્વાકર્ષણને કારણે થતું કાર્ય ..........$J$ થશે. [પાણીની ધનતા $=10^{3} \,kg / m ^{3}$ અને $g =10 \,ms ^{-2}$ લો.]View Solution
