\(U _{\max }=\frac{1}{2} L I _{ max }^{2}\)
\(i = I _{\max }\left(1- e ^{- Rt / L }\right)\)
For \(U\) to be \(\frac{ U _{\max }}{ n } ;\) i has to be \(\frac{ I _{ max }}{\sqrt{ n }}\)
\(\frac{I_{\max }}{\sqrt{n}}=I_{\max }\left(1-e^{-R t / L}\right)\)
\(e ^{- Rt / L }=1-\frac{1}{\sqrt{ n }}=\frac{\sqrt{ n }-1}{\sqrt{ n }}\)
\(-\frac{ Rt }{ L }=\ln \left(\frac{\sqrt{ n }-1}{\sqrt{ n }}\right)\)
\(t =\frac{ L }{ R } \ln \left(\frac{\sqrt{ n }}{\sqrt{ n }-1}\right)\)
Download our appand get started for free
Similar Questions
- 1જો $N$ કોઈલના આંટાની સંખ્યા હોય, તો તેનું આત્મપ્રેરકત્વ કઈ રીતે બદલાય?View Solution
- 2$2 \,\Omega$ અવરોધ ધરાવતી કોઇલમાં $0.2 \,sec$ માં ચુંબકીય ફલ્કસનો ફેરફાર $2.0 \,Wb$ થી $10.0 \,Wb$ કરતાં કેટલા ..........$coulomb$ વિદ્યુતભાર ઉત્પન્ન થાય?View Solution
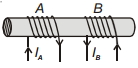
- 3સમાન લોખંડનાં સળીયા પર બે કોઈ $A$ અને $B$ વીંટાળવામાં આવેલ છે. અહી વિંટાળેલ ગુંચળાની સંખ્યા $N_A$ અને $N_B$ છે . તો સાચુ વિધાન જણાવો.View Solution
- 4View Solutionઆપેલ પરિપથ માટે, વપરાયેલ ટ્રાન્સફોર્મર માટે પ્રતિક્રિયા આપો :
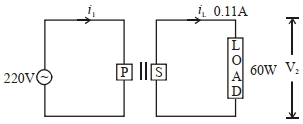
- 5View Solutionટ્રાન્સફોર્મર કયાં સિધ્દ્વાંત પર કાર્ય કરેં છે.
- 6ઈન્ડક્ટરને સ્વીચથી $DC$ વૉલ્ટેજ સપ્લાય સાથે જોડતા હવે,View Solution
- 7$8.4 \,mH$ ઇન્ડકટન્સ અને $6\,Ω$ અવરોઘ ઘરાવતી કોઇલને $12\, V$ સાથે જોડેલ છે. કોઇલમાં $1 \,A$ પ્રવાહ કેટલા સમય પછી પસાર થશે?View Solution
- 8સ્ટેપ અપ ટ્રાન્સફોર્મર $220 \,AC$ વોલ્ટેજનું $2200$ વોલ્ટેજમાં રૂપાંતર કરે છે.ગૌણ ગૂંચળામાં આંટાની સંખ્યા $2000$ હોય,તો પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા કેટલી હશે?View Solution
- 9એક બોટ પૂર્વ દિશામાં ગતિ કરી રહી છે.આ વિસ્તારમાં પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટક $5.0 \times 10^{-5}$ $NA^{-1}m^{-1}$ છે.બોટ પર ઊઘ્વદિશામાં $2$ $m$ લંબાઇનું એન્ટેના લગાવેલ છે.જો બોટની ઝડપ $1.5$ $ ms^{-1}$ હોય,તો એન્ટેનાના તારમાં પ્રેરિત $emf$ ......... $mV$ હશે.View Solution
- 10નીચે આપેલા વિધાનોમાંથી એક વિધાન $A$ છે અને બીજું વિધાન કારણ $R$ છે.View Solution
વિધાન $A:$ એક ગજિયા ચુંબકને જયારે ધાત્વીત નળાકારમાંથી પસાર કરવામાં આવે છે ત્યારે લાગતો સમય એક અચુંબકીય દંડા કે જે સમાન ભૂમિતિ અને દળ ધરાવે છે તેના કરતાં વધુ હોય છે.
કારણ $R:$ ગજિયા ચુંબક માટે ધાતુની નળીમાં એડી વીજપ્રવાહ ઉત્પન્ન થાય છે, કે જે ગંજિયા ચુંબકની ગતિને અવરોધે છે.
ઉપરોક્ત સત્યાર્થતા ને આધારે, સાચો જવાબ નીચેના વિકલ્પોમાંથી પસંદ કરો.
