Initial angular momentum = \(I{\omega _1} + I{\omega _2} \)
Let \(\omega \) be angular speed of the combined system.
Final angular momentum \(=2I\)\(\omega \)
\(\therefore \) According to conservation of angular momentum
\(I{\omega _1} + I{\omega _2} = 2I\omega \,\,or\,\,\omega = \frac{{{\omega _1} + {\omega _2}}}{2}\)
Initial rotational kinetic energy
\(E = \frac{1}{2}I\left( {\omega _1^2 + \omega _2^2} \right)\)
Final rotational kinetic energy
\(\begin{array}{l}
{E_f} = \frac{1}{2}\left( {2I} \right){\omega ^2} = \frac{1}{2}\left( {2I} \right){\left( {\frac{{{\omega _1} + {\omega _2}}}{2}} \right)^2}\\
\,\,\,\,\,\,\,\, = \frac{1}{4}I{\left( {{\omega _1} + {\omega _2}} \right)^2}\\
\therefore \,Loss\,of\,energy\,\Delta E = {E_i} - {E_f}\\
\,\,\,\,\,\, = \,\frac{1}{2}\left( {\omega _1^2 + \omega _2^2} \right) - \frac{I}{4}\left( {\omega _1^2 + \omega _2^2 + 2{\omega _1}{\omega _2}} \right)\\
\,\,\,\,\,\, = \frac{I}{4}\left[ {\omega _1^2 + \omega _2^2 - 2{\omega _1}{\omega _2}} \right] = \frac{I}{4}{\left( {{\omega _1} - {\omega _2}} \right)^2}
\end{array}\)
Download our appand get started for free
Similar Questions
- 1$h$ ઊંચાઇના ઢાળ પરથી ઘન નળાકાર મૂકતાં ચાકગતિઉર્જા અને કુલઉર્જાનો ગુણોત્તરView Solution
- 2આકૃતિમાં દર્શાવ્યા અનુસાર $R$ ત્રિજયા અને $9$ $M$ દળ ધરાવતી સમાન વર્તુળાકાર તકતીમાંથી નાની $\frac{R}{3}$ ત્રિજયાની સમકેન્દ્રિય તકતી દૂર કરવામાં આવેલ છે. તકતીના સમતલને લંબ અને તકતીના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષી બાકી રહેલ તકતીની જડત્વની ચાકમાત્રા ___View Solution
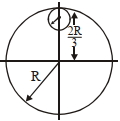
- 3એક પૈડું તેની ભૌમિતિક અક્ષને અનુલક્ષીને $ 60\ rpm$ ની ઝડપથી ભ્રમણ કરે છે. જો આ અક્ષને અનુલક્ષીને પૈડાની જડત્વની ચાકમાત્રા $2\ kg m^2$ હોય,તો તેના ઉપયુક્ત ભ્રમણને એક મિનિટમાં રોકવા કેટલું ટોર્ક જોઇએ ?View Solution
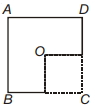
- 4એક નિયમિત ચોરસ પ્લેટ માંથી નીચે બતાવ્યા પ્રમાણે $1 / 4$ ભાગ દૂર કરવામાં આવે છે. બાકી બચેલા ભાગનું દ્રવ્યમાન કેન્દ્ર ......... પર હશે ?View Solution
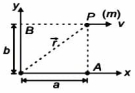
- 5એક કણ $x$ -અક્ષને સમાંતર સીધી રેખામાં અયળ વેગથી ગતિ કરી રહ્યો છે. સદિશ સ્વરૂપમાં ઊગમ બિંદુને અનુલક્ષીને કોણીય વેગમાન શોધો.View Solution
- 6$2\ kg $ દળ ધરાવતો એક દઢ પદાર્થ $ 0.8\ m$ ત્રિજ્યા ધરાવતા, એક વર્તૂળાકાર પથ પર $44 \ rad s^{-1 }$ ના કોણીય વેગથી ગતિ કરે છે. જો આ વર્તૂળાકાર પથની ત્રિજ્યા $1 \ m $ થાય, તો આ પદાર્થનો નવો કોણીય વેગ ........ $rad\, s^{-1}$ થાય.View Solution
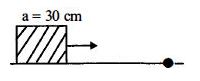
- 7$30\,cm$ બાજુ ધરાવતું ઘન ચોસલું લીસ્સી સમક્ષિતિજ સપાટી પર $2\,\,ms^{-1}$ વેગથી ગતિ કરે છે. આકૃતિમાં બતાવ્યા મુજબ સપાટીમાં બિંદુ $O$ પર ટેકરો છે. તો ટેકરા સાથે અથડામણ બાદ તરત જ ચોસલાનો કોણીય વેગ કેટલો હશે?View Solution
- 8$30^o $ ના ખૂણાવાળા ઢાળ પર પોલો નળાકાર મૂકતાં $10\ m$ અંતર કાપ્યા પછી તેનો વેગ.......... $m/s$View Solution
- 9જો એક પૈડું $2000$ ભ્રમણ માં $9.5\ km$ અંતર કાપ્તુ હોય તો પૈડાનો વ્યાસ કેટલો હોય ?View Solution
- 10View Solutionનીચેનામાંથી કયા પદાર્થમાં વ્યાસ પર લંબ અક્ષ પ્રમેય વડે જડત્વની ચાકમાત્રા શોધી શકતી નથી?
