Therefore the coordinates of centre of mass are.
\(x_{\alpha n}=\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}+m_{4} x_{4}}{m_{1}+m_{2}+m_{3}+m_{4}}=\frac{M(o)+2 M\left(\frac{a}{2}\right)+3 M\left(\frac{3 a}{2}\right)+a M(a)}{M+2 M+3 M+4 M}\)
\(\Rightarrow x_{c m}=\frac{\frac{M a}{2}+\frac{9 M A}{2}+\frac{8 M a}{2}}{10 M}=\frac{9 M a}{10 M}\)
\(\Rightarrow x_{c m}=\frac{9 a}{10}\)
\(y_{c n}=\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}+m_{4} y_{4}}{m_{1}+m_{2}+m_{3}+m_{4}}=\frac{M(0)+2 M\left(\frac{\sqrt{3} a}{2}\right)+3 M\left(\frac{\sqrt{3} a}{2}\right)+4 M(0)}{M+2 M+3 M+4 M}\)
\(y_{c m}=\frac{\frac{5 \sqrt{3 M a}}{2}}{10 M}=\frac{5 \sqrt{3} M a}{20 M}\)
\(\Rightarrow y_{c m}=\frac{\sqrt{3 a}}{4}\)
Therefore, the coordinates of the centre of mass are.
\(\left(x_{c m} \cdot y_{c m}\right)=\left(\frac{9 a}{10}, \frac{\sqrt{3} a}{4}\right)\)
Download our appand get started for free
Similar Questions
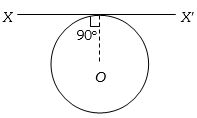
- 1$L$ લંબાઇ અને $\rho $ રેખીય ઘનતા ધરાવતા તારને વર્તુળમાં વાળતાં $XX'$ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 2$M $ દળ અને $ l $ લંબાઇના ચાર પાતળા સળિયા એક ચોરસ ફ્રેમની રચના કરે છે. આ ચોરસના સમતલને લંબ અને ફ્રેમના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
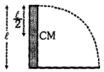
- 3View Solutionપાતળી મીટર પટ્ટીનો એક છેડો જમીન પર રહે તેમ ગોઠવેલી છે એક છેડાનો સંપર્ક સ્થાયી રહે તેમ નીચે પડવા દેવામાં આવે છે તો તેની સૌથી ઉપરના છેડો જમીનને અથડાય ત્યારે વેગ શોધો.
- 4એક દોરીને $0.40 \mathrm{~kg} \mathrm{~m}^2$ જેટલી જડત્વની ચાકમાત્રા અને $10 \mathrm{~cm}$ ની ત્રિજ્યા ધરાવતા પૈડાની ધરીને ફરતે વીંટાયેલી છે. પૈડું તેની અક્ષને ફરતે મુક્ત રીતે ફ઼રી શકે છે. પ્રારંભમાં પૈડું વિરામસ્થિતિમાં છે. દોરીને હવે $40 \mathrm{~N}$ ના બળથી ખેંચવામાં આવે છે. $10 \mathrm{~s}$ પછી પૈડાનો કોણ઼ીય વેગ $x \ \mathrm{rad} / \mathrm{s}$ છે ક્યાં $x$ ................ થશે.View Solution
- 5એક પદાર્થ માત્ર કોણીય ગતિ કરે છે જો કણ નો રેખીય વેગ $v$ અને તે $x$-અક્ષ થી $r$ અંતરે $\omega $ કોણીય વેગ થી ફરતો હોય $\omega = \frac{v}{r}$ હોય તો પદાર્થ માટે શું સાચું છે ?View Solution
- 6$20\ g$, $30\ g$ અને $50\ g$ દળના કણનો વેગ અનુક્રમે $10 \vec i,\,10\vec j,\,$ અને $\,10\vec k$ છે. તો આ ત્રણેય કણના દ્રવ્યમાનકેન્દ્રનો વેગ કેટલો થાય ?View Solution
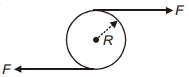
- 7નીયે દર્શાવ્યા પ્રમાણે એક $M$ દળ અને $R$ ત્રિજ્યા વાળી એક નિયમિત તક્તી ઉપર બે સમાન અને વિરુદ્ધ દિશામાંંના બળો સ્પર્શકીય રીતે લગાડવામાં આવે છે. જો તક્તીને તેના કેન્દ્ર પર કિલકીત કરેલી હોય અને તેના સમતલમાં મુક્ત પણે ભ્રમણ કરાવવામાં આવે તો તકતીનો કોણીય પ્રવેગ શું થાય?View Solution
- 8સમાન જડત્વની ચાકમાત્રા ધરાવતી બે તકતીઓ ની કોણીય ઝડપ ${\omega _1}\;$અને$\;{\omega _2}$છે,આ બંને તકતીઓની અક્ષ એક કરી દેવામાં આવે,તો ઊર્જાનો વ્યયView Solution
- 9એક વર્તુળાકાર તકતી $L$ લંબાઈના ઢાળ પરથી ઉપરથી નીચે આવે છે, જ્યારે તે ઢાળ પર સરકીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{1}$ છે. જ્યારે તે ગબડીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{2}$ છે. તો $\frac{t_{2}}{t_{1}}$ નું મૂલ્ય $\sqrt{\frac{3}{x}}$ છે, તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 10$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીની કોણીય ઝડપ $\omega_{1}$ છે. બીજી $\frac{ R }{2}$ ત્રિજ્યા અને $M$ દળ ધરાવતી તકતી તેના પર મુક્તા નવી કોણીય ઝડપ $\omega_{2}$ છે.શરૂઆતની ઊર્જાનો વ્યય થાય તો $p=.......$View Solution
