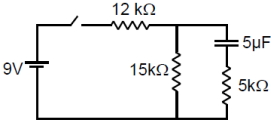
$t=\infty$ સમયે કળ ખુલ્લી કરતા $1$ સેકન્ડ પછી કેપેસિટર પર વિદ્યુતભાર શોધો.

AIIMS 2019, Diffcult
b
When the time \(t=\infty,\) the current is,
When the time \(t=\infty,\) the current is,
\(i=\frac{9}{27 \times 10^{3}}\)
The voltage is given by,
\(V_{c}=i \times 15 \times 10^{3}\)
The initial charge is given by,
\(q_{0}=5 \times 10^{-6} \times \frac{9}{27} \times 15\)
\(=25 \mu C\)
The charge when switch is open is given by,
\(q=q_{0} e^{\frac{-t}{R C}}\)
Substitute \(25 \mu C\) for \(q_{0}, 1\) sec for \(t, 20 \times 10^{3}\) for \(R\) and \(5 \times 10^{-6}\) for \(C\) in equation \((I).\)
\(q=(25 \mu C ) e^{\frac{-(1 \sec )}{\left(20 \times 10^{3}\right)\left(5 \times 10^{-6}\right)}}\)
\(=25 e^{-10} \mu C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પોટેન્શીયોમીટરના તારની લંબાઈ $100\ cm$ છે અને તેના સ્ટેન્ડ અને સેલ કોષનું $emf\ E$ વોલ્ટ છે. તે જેનો આંતરિક અવરોધ $0.5\, \Omega$ હોય તેવી બેટરીનું $emf$ માપવા માટેનો ઘટક છે. જે સંતુલન બિંદુ ધન છેડાથી $ℓ = 30\, cm$ અંતરે મળતું હોય તો બેટરીનું $emf$ ........છે.View Solution
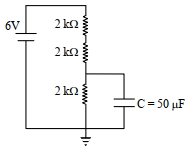
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે પરિપથ સાથે $50 \,\mu {F}$ નું કેપેસીટર જોડેલું છે, તો કેપેસીટરની ઉપરની પ્લેટ પરનો વિજભાર કેટલા $\mu {C}$ હશે?View Solution
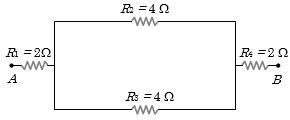
- 3View Solutionનીચે આપેલ પરિપથમાં કયા પરિપથનો પાવર મહત્તમ થશે?
- 4View Solutionનીચે આપેલ પરિપથમાં કયા પરિપથનો પાવર મહત્તમ થશે?
- 5મીટરબ્રીજમાં બે ગેપમાં અનુક્રમે $10\, \Omega$ અને $30 \,\Omega$ નાં અવરોધ છે. આ અવરોધોની અદલા બદલી કરતાં તટસ્થ બિંદુ.....સેમી ખસશે.View Solution
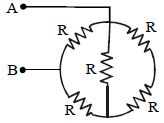
- 6$A$ અને $B$ વચ્ચે સમતુલ્ય અવરોધ ........... $\Omega$View Solution
- 7એક અર્ધવાહકમાં ઇલેકટ્રૉનની સંખ્યા અને હોલની સંખ્યાનો ગુણોત્તર $7/5 $ અને તેમના પ્રવાહનો ગુણોત્તર $7/4$ છે, તો તેમના ડ્રિફટ વેગનો ગુણોત્તર કેટલો હશે ?View Solution
- 8$120 \ V, 60\ W$ નાં વિધુત લેમ્પના ફિલામેન્ટમાંથી એક સેકન્ડમાં વહેતા ઈલેક્ટ્રોનની સંખ્યા શોધો.View Solution
- 9તારનો અવરોધ $R\; ohm$ છે. જો તારને ઓગાળવામાં આવે અને ખેંચીને લંબાઇ મૂળ લંબાઈ કરતાં $n$ ગણી કરતાં નવો અવરોઘ કેટલો થશે?View Solution
- 10$A$ અને $B$ વચ્ચે પરિપથનો સમતુલ્ય અવરોધ ..... .View Solution