\(R(T)=R_{o}\left(1+\alpha\left(T-T_{o}\right)\right)\)
Applying boundary conditions, \(120=100(1+200 \alpha)\)
\(\alpha=10^{-3} \,K^{-1}\)
It is given that temperature increases at a constant rate from \(300\, \mathrm{K}\) to \(500 \,\mathrm{K}\) in \(30\, \mathrm{s}\). Hence, \(T(t)=300+20 t / 3\)
By Joule's Law, heat dissipated in a resistor is given by:
\(W=\int_{0}^{30} \frac{V^{2}}{R} d t\)
\(=\int_{0}^{30} \frac{V^{2}}{R_{0}\left(1+\alpha\left(T-T_{0}\right)\right)} d t\)
\(=\frac{V^{2}}{R_{o}} \int_{0}^{30} \frac{1}{(1+20 \alpha t / 3)} d t\)
Solving, \(W=400 \ln (6 / 5)\)
Work done on resistor \(=-W=400 \ln (5 / 6) \,J\)
Download our appand get started for free
Similar Questions
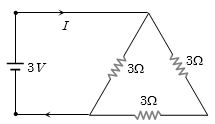
- 1આપેલ પરિપથને $3\, volt$ અને અવગણ્ય આંતરિક અવરોધ ધરાવતી બેટરી સાથે જોડેલ છે. તો તેમાંથી પસાર થતો પ્રવાહ $I$ કેટલા $A$ નો હશે?View Solution
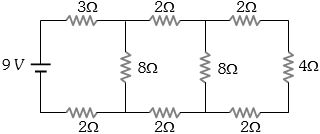
- 2View Solutionઆપેલ પરિપથમાં....
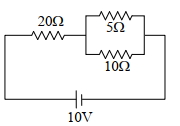
- 3નીચે આપેલ પરિપથમાં $5 \Omega$ અને $10 \Omega$ અવરોધમાં વિખેરણ પામતી ઊર્જાઓનો ગુણોત્તર . . . . .હશે.View Solution
- 4$A$ અને $B$ વચ્ચે પોટેન્શિયોમીટર જોડતા સંતુલિત બિંદુ $203. 6$ સેમી પર મળે છે.જ્યારે પોટેન્શિયોમીટરના છેડાને $B$ થી $C$ પર જોડતા સંતુલિત બિંદુ મળે છે.જો પોટેન્શિયોમીટરને $B$ અને $C$ વચ્ચે જોડતા સંતુલિત બિંદુ ...... સેમી પર મળેView Solution
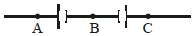
- 5નીચે બે કથનો આપેલા છેView Solution
કથન $I:$ અવરોધોના શ્રેણી સંયોજનનો સમતુલ્ય અવરોધ સંયોજનમાં વપરાતા ન્યૂનત્તમ અવરોધ કરતા નાનો હોય છે.
કથન $II:$ દ્રવ્યની અવરોધકતા તાપમાનથી સ્વતંત્ર છે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
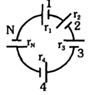
- 6આકૃતિમાં બતાવ્યા પ્રમાણે $N$ કોષોનો સમૂહ કે જેમનું $emf\ E_N = 1.5\ r_N$ સૂત્ર પ્રમાણે આંતરિક અવરોધ સાથે બદલાય છે. પરિપથમાં પ્રવાહ $I$ ................ $A$ છે.View Solution
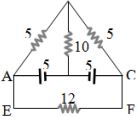
- 7આપેલ પરીપથમાં $12\, \Omega$ અવરોધમાંથી પસાર થતો પ્રવાહ............ $A$ હશે.View Solution
- 8અવરોધના દ્રવ્યનો રેખીય વિસ્તરણ ગુણાંક $\alpha$ છે. તેની અવરોધક્તા અને અવરોધનો તાપમાન ગુંણાક અનુક્રમે $\alpha_p$ અને $\alpha_R$ હોય, તો સાચો સંબંધ પસંદ કરો.View Solution
- 9View Solutionઇલેક્ટ્રોપ્લેટીંગ કઈ પરિસ્થિતીમાં મદદ કરે નહીં
- 10$R_1 $ અને $ R_2 $ અવરોધના શ્રેણી અને સમાંતરના સમતુલ્યનો ગુણોત્તર $n$ હોય,તો...View Solution
