$V$ વોલ્ટથી ચાર્જ કરેલા કેપેસિટર $C$ ને $2V$ વોલ્ટેજથી ચાર્જ કરેલાં કેપેસિટર $2C$ સાથે સમાંતરમાં જોડતાં તંત્રની અંતિમ ઊર્જા કેટલી થાય?
IIT 1995, Medium
Download our app for free and get started
c
(c) Total charge \( = (2C)\,(2V) + (C)\,( - V) = 3CV\)
Common potential \( = \frac{{3CV}}{{3C}} = V\)
Energy \( = \frac{1}{2}(3C)\,{(V)^2} = \frac{3}{2}C{V^2}\)
(c) Total charge \( = (2C)\,(2V) + (C)\,( - V) = 3CV\)
Common potential \( = \frac{{3CV}}{{3C}} = V\)
Energy \( = \frac{1}{2}(3C)\,{(V)^2} = \frac{3}{2}C{V^2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યારે એક ઇલેક્ટ્રોનને બીજા ઇલેક્ટ્રોન તરફ લઈ જવામાં આવે, ત્યારે તંત્રની વિદ્યુતસ્થિતિઊર્જા ....
- 2શૂન્યાવકાશમાં $3\, cm$ તથા $1\, cm$ ત્રિજ્યાવાળા ગોળાને એકબીજાથી $10\, cm$ અંતરે રાખેલ છે જો દરેક ગોળાઓને $10\, V$ જેટલો વિદ્યુતભારીત કરવામાં આવે તો તેમની વચ્ચેનું અપાકર્ષણ બળ....View Solution
- 3અવરોધ $R$ અને $2\; \mu F$ કેપેસીટન્સ વાળા કેપેસીટરને $200\;V$ ના સ્ત્રોત સાથે શ્રેણીમાં જોડવામાં આવે છે. કેપેસીટરને સમાંતર નિયોન બલ્બ જોડવામાં આવે છે, જે $120\;V$ ના વિદ્યુતસ્થિતિમાનનો તફાવત હોય તો ચાલુ થઈ શકે છે. જો સ્વીચ બંધ કર્યા બાદ $5 \;s$ સુધી બલ્બ ચાલુ રાખવો હોય, તો અવરોધ $R$ નું મૂલ્ય કેટલું હોવું જોઈએ ?View Solution
$(log_{10} 2.5 = 0.4)$.
- 4ઉગમબિંદુથી $R_o$ અંતરે એક સમાન ગોલીય સંમિતિ ધરાવતી પૃષ્ઠ વિધુતભાર ઘનતા રહેલ છે. વિદ્યુતભાર વિતરણ પ્રારંભમાં સ્થિર છે, અને પછી તેનું પરસ્પર અપાકર્ષણ થવાને કરાણે સમાન રીતે વિસ્તરણ થાય છે. વિસ્તરણ માટે તેની તત્ક્ષણિક ત્રિજ્યા $R(t)$ ના વિધેય તરીકે ઝડપ $V(R(t))$ ને રજુ કરતી આકૃતિ નીચેનામાથી કઈ છે.View Solution
- 5એક ક્ષેત્રમાં એકસમાન વિદ્યુતક્ષેત્ર પ્રવર્તે છે. આ ક્ષેત્રમાં બિંદુ $P$ આગળ કેન્દ્ર હોય તેવા ગોળા પરના અલગ અલગ બિંદુ આગળનું વિદ્યુતસ્થિતિમાન $589.0\,V$ થી $589.8\, V$ જેટલું બદલાય છે. વિદ્યુતક્ષેત્ર સાથે $60^o$ નો ખુણો બનાવતા સ્થાન સદીશ પર રહેલ ગોળા પરના બિંદુ આગળ વિદ્યુતસ્થિતિમાન ($V$ માં) કેટલું હશે?View Solution
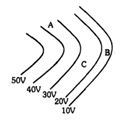
- 6આકૃતિ આપેલ પ્રદેશમાં અચળ સ્થિતિમાનની રેખાઓ દર્શાવે છે કે જ્યાં વિદ્યુતક્ષેત્ર હાજર હોય. $B$ બિંદુએ વિદ્યુતક્ષેત્ર............ છે.View Solution
- 7$12\ \mu C$ અને $8\ \mu C$ ના બે બિંદુવત ધન વિદ્યુતભાર $10\, cm$ દૂર આવેલા છે. તેમને $4 \,cm$ નજીક લાવતાં થતું કાર્ય ......છે.View Solution
- 8આપેલ સમાંતર પ્લેટ કેપેસીટરના તંત્રને અમુક વિદ્યુતસ્થિમાનના તફાવત વચ્ચે મુકેલ છે. જ્યારે $3\, mm$ જાડાઈ ધરાવતા બ્લોકને કેપેસીટરની પ્લેટ વચ્ચે મૂકવામાં આવે ત્યારે તંત્રમાં સમાન વિદ્યુતસ્થિમાનનો તફાવત જાળવી રાખવા માટે પ્લેટ વચ્ચેના અંતરમાં $2.4\, mm$ જેટલો વધારો કરવામાં આવે છે. તો બ્લોકના દ્રવ્યનો ડાઈઇલેક્ટ્રિક અચળાંક કેટલો હશે?View Solution
- 9$100\, micro-farad$ કેપેસિટન્સ ધરાવતા કેપેસિટરની પ્લેટ પર $8 \times {10^{ - 18}}\, C$ વિદ્યુતભાર મૂકવા માટે કેટલું કાર્ય કરવું પડે?View Solution
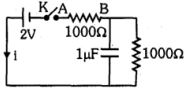
- 10$t = 0$ સમયે જ્યારે કળને દબાવવામાં આવે છે ત્યારે આપેલા પરિપંથમાં $AB$ અવરોધમાંના $'i'$ વિદ્યુતપ્રવાહ માટે નીચેનામાંથી કયું વિધાન સાચું છે ?View Solution
