યંગના પ્રયોગમાં, જયાં પથતફાવત $\lambda$ . હોય ત્યાં તીવ્રતા $k$ છે.જયાં પથતફાવત $\lambda /4$ હોય ત્યાં તીવ્રતા કેટલી હશે? ( $λ=$ પ્રકાશની તરંગલંબાઇ)
Medium
b
\(\phi = \frac{{2\pi }}{\lambda }(\Delta )\)
\(\phi = \frac{{2\pi }}{\lambda }(\Delta )\)
\(\lambda , {\phi _1} = 2\pi \)
\( \lambda /4, \phi_2 = \pi/2.\)
\(I = 4{I_0}{\cos ^2}\frac{\phi }{2}\)
==> \(\frac{{{I_1}}}{{{I_2}}} = \frac{{{{\cos }^2}({\varphi _1}/2)}}{{{{\cos }^2}({\phi _2}/2)}}\)
==> \(\frac{k}{{{I_2}}} = \frac{{{{\cos }^2}(2\pi /2)}}{{{{\cos }^2}\left( {\frac{{\pi /2}}{2}} \right)}} = \frac{1}{{1/2}}\)
==> \({I_2} = \frac{k}{2}.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ડબલ સ્લિટના પ્રયોગમાં પ્રથમ અધિકતમ અને પાંચમાં ન્યુનતમ વચ્ચેનું અંતર $7\,mm$ હોય અને સ્લીટ વચ્ચે અંતર $0.15\,mm$ અને સ્લીટથી પડદાનું અંતર $50\,cm$ હોય, તો વપરાયેલા પ્રકાશની તરંગલંબાઈ $............\,nm$View Solution
- 2બે સ્લિટથી વ્યતિકરણ મેળવવામાં આવે છે. જો કેટલાક પડદાના બિંદુઓ પાસે પીળા પ્રકાશનો પથ તફાવત $3\, \lambda/2$ હોય, તો તે બિંદુ પાસે શલાકા . . . . . .View Solution
- 3ચાર સ્વતંત્ર તરંગો નીચેના સમીકરણોથી દર્શાવાય છે. તો ક્યા સમીકરણ વ્યતિકરણની ઘટના દર્શાવે છે?$Y_1 = a_1 \,sin\,\omega t, \,Y_2\, = a_2 \,sin\,\omega t,\, Y_3 = \,a_3\, cos\,\omega t, $ ${Y_4}\, = \,\,{a_4}\,\,\sin \,\,\,(\omega t\, + \,\,\frac{\pi }{3})$View Solution
- 4$670 \,nm$ જેટલી ચોકકસ તરંગ લબાઈ ($v$ વેગથી ગતિ કરતી પ્રકાશગંગામાંથી આવતો પ્રકાશ) માટે અવલોકાતી તરંગલંબાઇ $670.7 \,nm$ છે.તો $v$ નું મુલ્ય કેટલું હશે?View Solution
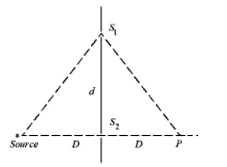
- 5આફૃતિમાં દર્શાવ્યા મુજબના બે સ્લિટના પ્રયોગમાં જ્યારે $400 \mathrm{~nm}$ તરંગ લંબાઈનો પ્રકાશ વાપરવામાં આવે, ત્યારે $P$ બિંદુએ અપ્રકાશિત શલાકા દેખાય છે. જો $D=0.2 \mathrm{~m}$ હોય તો સ્લિટ $S_1$ અને $S_2$ વચ્ચેનું લધુત્તમ અંતર_________ $\mathrm{mm}$ છે.View Solution
- 6યંગના પ્રયોગમાં મહત્તમ તીવ્રતા $I $ છે,એક સ્લિટ બંધ કરતાં મહત્તમ તીવ્રતા $I_0$ છે,તો નીચેનામાથી શું સાચું થાય?View Solution
- 7સમતલ કાચની પ્લેટ ઉપર સમતલ બહિર્ગોળ લેન્સની બહિર્ગોળ સપાટી મૂકીને હવાની પાતળી ફિલ્મ (સ્તર) રચેલ છે. એકરંગી પ્રકાશ સાથે આ પાતળી ફિલ્મ સૌથી ઉપરની બહિર્ગોળ સપાટી અને નીચેની કાચની સપાટી પરથી થતા પરાવર્તનના લીધે વ્યતિકરણ રચના આપે છે.View Solution
વિધાન : $1$ : જ્યારે પ્રકાશ હવા -કાચની પ્લેટમાંથી પરાવર્તિત થઈને વ્યતિકરણ પામે છે. તો પરાવર્તિત તરંગ જેટલો કળા તફાવત આપે છે.
વિધાન : $2$: વ્યતિકરણ ભાતનું કેન્દ્ર અપ્રકાશિત છે.
- 8સિંગલ સ્લીટ વિવર્તનના પ્રયોગમાં મુખ્ય મધ્યમાન શલાકાની તીવ્રતા ${I_0}$ હોય તો સ્લીટની પહોળાઈ બમણી કરવામાં આવે તો તીવ્રતા કેટલી થાય?View Solution
- 9View Solutionધ્વનિ તરંગ અને પ્રકાશ તરંગ વચ્ચે સામ્યતા કઈ છે?
- 10યંગના પ્રયોગમાં $t$ જાડાઈની અને $\mu$ વક્રીભવનાંક ધરાવતી પારદર્શક તકતી એક સ્લીટના માર્ગમાં મૂકવાથી મધ્યમાન પ્રકાશિત શલાકાનું $n$ શલાકાની જાડાઈ જેટલું સ્થાનાંતર થાય છે.વપરાયેલ પ્રકાશની તરંગલંબાઈ $\lambda$ હોય તો તકતીની જાડાઈ $t$ કેટલી હશે?View Solution