વ્યતિકરણ ઘટનામાં \(I\,\, = \,\,{I_1} + \,\,{I_2}\, + \,\,2\,\sqrt {{I_1}{I_2}\,\,\cos \,\,\phi } \)
\(I\) ના મહત્તમ અને ન્યૂનત્તમ મૂલ્ય માટે \(cos\, \theta \) અનુક્રમે \(1\) અને \(-1\) છે.
\(I\) મહતમ \( = \,\,\,{I_1} + {I_2}\,\, + \,\,2\,\,\sqrt {{I_1}{I_2}} \,\, = \,\,\,{\left( {\sqrt {{I_1}} + \sqrt {{I_2}} } \right)^2}\) અને \(I\) ન્યૂનતમ \( = \,\,\,{I_1} + {I_2} - \,\,2\sqrt {{I_1}{I_2}} \,\, = \,\,\,{\left( {\sqrt {{I_1}} - \sqrt {{I_2}} } \right)^2}\)
\(I\) મહતમ/ \(I\) ન્યૂનતમ \( = \,\,\,\frac{{{{\left( {\sqrt {{I_1}} + \sqrt {{I_2}} } \right)}^2}}}{{{{\left( {\sqrt {{I_1}} - \sqrt {{I_2}} } \right)}^2}}}\,\,\, = \,\,\,\frac{9}{1}\,\, \Rightarrow \,\,\frac{{\sqrt {{I_1}} + \sqrt {{I_2}} }}{{\sqrt {{I_1}} - \sqrt {{I_2}} }}\,\, = \,\,\,\frac{3}{1}\)
યોગ અને વિયોગ પ્રમાણે \(\,\frac{{\sqrt {{I_1}} }}{{\sqrt {{I_2}} }}\,\, = \,\,\,\frac{{3 + 1}}{{3 - 1}}\,\, = \,\,\frac{2}{1}\,\,\, \Rightarrow \,\,\frac{{{I_1}}}{{{I_2}}}\,\, = \,\,4\)
Download our appand get started for free
Similar Questions
- 1તારામાંથી આવતા પ્રકાશની તરંગલંબાઈ $\lambda$ છે. $r$ વ્યાસનો વસ્તુકાચ ધરાવતા દૂરબીનની વિભેદનની હદ કેટલી છે ?View Solution
- 2View Solutionયંગના પ્રયોગમાં ઇલેકટ્રોન બીમનો ઉપયોગ કરવામાં આવે છે,જો ઇલેકટ્રોનની ઝડપ વધારતાં...
- 3યંગના પ્રયોગમાં, જયાં પથતફાવત $\lambda$ . હોય ત્યાં તીવ્રતા $k$ છે.જયાં પથતફાવત $\lambda /4$ હોય ત્યાં તીવ્રતા કેટલી હશે? ( $λ=$ પ્રકાશની તરંગલંબાઇ)View Solution
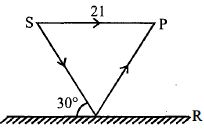
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે ઉદગમ $S$ માંથી નિકળતા બે કિરણના સંપાતિકરણથી બિંદુ $P$ આગળ વ્યતિકરણની ભાત જોવા મળે છે. તો બિંદુ $P$ આગળ મળતી મહત્તમ તીવ્રતા $I$ નું મૂલ્ય કેટલું હશે? ($R$ એ સંપૂર્ણ પરાવર્તિક સપાટી છે)View Solution
- 5બે સ્લિટના પ્રયોગમાં $400\,nm$ તરંગલંબાઈના પ્રકાશ માટે પડદા પર શલાકાની પહોળાઈ $2\,mm$ છે. $600\,nm$ તરંગ લંબાઈના પ્રકાશ માટે શલાકાની પહોળાઈ $..........\,mm$ થશે.View Solution
- 6$0.2 \mathrm{~mm}$ પહોળાઈ ધરાવતી સ્લિટ પરથી $400 \mathrm{~nm}$ તરંગલંબાઈ ધરાવતા પ્રકાશથી વિવર્તન માટે મળતી વિવર્તન ભાત ને $100 \mathrm{~cm}$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સની મદદથી ફોકલ સમતલ (મુખ્ય સમતલ) પર કેન્દ્રિત (ફોક્સ) કરવામાં આવે છે. પહેલાં દ્વિતીય મહત્તમોની પહોળાઈ_________થશે.View Solution
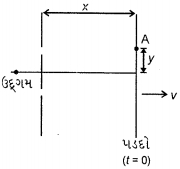
- 7યંગના બે સ્લિટના પ્રયોગમા પડદો $v$ જેટલી અચળ ઝડપે જમણી બાજુ ખસે છે. સ્લિટના સમતલ અને પડદા વચ્ચે શરૂઆતનુ અંતર $x$ છે. $t=0$ સમયે પહેલા ક્રમનુ મહતમ બિંદુ $A$ પાસે છે. કેટલા સમય પછી બિંદુ $A$ પાસે પ્રથમ ક્રમનુ લઘુતમ હશે.View Solution
- 8વક્રીભવનાંક $\mu =1.5$ અને જાડાઈ $ t =2.5 \times10^{-5} m$ ધરાવતા પારદર્શક માધ્યમને યંગના સ્લીટના પ્રયોગમાં સ્લીટ આગળ મૂકવામાં આવે છે. તો વ્યતિકરણ ભાત કેટલી ખસશે ($cm$ માં)?View Solution
બે સ્લીટ વચ્ચેનું અંતર $ 0.5 \,mm $ અને પડદા અને સ્લીટ વચ્ચેનું અંતર $100\, cm$ છે.
- 9View Solutionબે ઉદ્ગમોને સુસંબદ્વ કયારે કહેવાય?
- 10View Solutionકોમ્પેક્ટ ડિસ્ક પર સફેદ પ્રકાશ આપાત કરતા રંગબેરંગી દેખાવાનું કારણ
