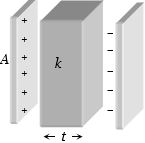
$A$ પ્લેટનું ક્ષેત્રફળ અને બે પ્લેટ વચ્ચેનું અંતર $d$ હોય,એવા કેપેસિટરમાં $t$ જાડાઇનું અને $k$ ડાઇઇલેકિટ્રક દાખલ કરતાં નવો કેપેસિટન્સ કેટલો થાય?
Diffcult
c
(c) Potential difference between the plates \(V = V_{air} + V_{medium}\)
\( = \frac{\sigma }{{{\varepsilon _0}}} \times (d - t) + \frac{\sigma }{{K{\varepsilon _0}}} \times t\)
\(==>\) \(V = \frac{\sigma }{{{\varepsilon _0}}}(d - t + \frac{t}{K})\)
\( = \frac{Q}{{A{\varepsilon _0}}}(d - t + \frac{t}{K})\)
Hence capacitance \(C = \frac{Q}{V} = \frac{Q}{{\frac{Q}{{A{\varepsilon _0}}}(d - t + \frac{t}{K})}}\)
\( = \frac{{{\varepsilon _0}A}}{{(d - t + \frac{t}{k})}} = \frac{{{\varepsilon _0}A}}{{d - t\,\left( {1 - \frac{1}{k}} \right)}}\)
(c) Potential difference between the plates \(V = V_{air} + V_{medium}\)
\( = \frac{\sigma }{{{\varepsilon _0}}} \times (d - t) + \frac{\sigma }{{K{\varepsilon _0}}} \times t\)
\(==>\) \(V = \frac{\sigma }{{{\varepsilon _0}}}(d - t + \frac{t}{K})\)
\( = \frac{Q}{{A{\varepsilon _0}}}(d - t + \frac{t}{K})\)
Hence capacitance \(C = \frac{Q}{V} = \frac{Q}{{\frac{Q}{{A{\varepsilon _0}}}(d - t + \frac{t}{K})}}\)
\( = \frac{{{\varepsilon _0}A}}{{(d - t + \frac{t}{k})}} = \frac{{{\varepsilon _0}A}}{{d - t\,\left( {1 - \frac{1}{k}} \right)}}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સુવાહક ગોળાના કેન્દ્રથી $R/2$ અંતરે સ્થિતિમાન ....... હશે.View Solution
- 2$30 \,cm$ અને $5 \,cm$ ત્રિજ્યાના બે સમકેન્દ્રી વાહક ગોલીય કવચ વિદ્યુતભારિત કર્યા છે. જો બાહ્ય કવચ પર $3\ \mu c$ અને આંતરિક કવચ પર $0.5\ \mu c$ વિદ્યુતભાર હોય તો બાહ્ય ગોલીય કવચ પરનું વિદ્યુત સ્થિતિમાન કેટલું થશે?View Solution
- 3$10^{-3}\;\mu C$ ના વિદ્યુતભારને $x - y$ યામપદ્ધતિના ઉગમબિંદુ પર મૂકેલો છે. બે બિદુઓ $A (\sqrt{2}, \sqrt{2})$ અને $B (2,0)$ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત ($V$ માં) કેટલો હશે?View Solution
- 4$100\, m ^{2}$ ક્ષેત્રફળ અને $10\, m$ બે પ્લેટ વચ્ચેનું અંતર ધરાવતાં સમાંતર પ્લેટ કેપેસિટર છે,તેમાં $5\,m$માં ડાઇઇલેક્ટ્રીક અચળાંક $10$ ધરાવતા ડાઇઇલેક્ટ્રીક મુક્તા નવા કેપેસિટન્સ $'x'$ $pF$ હોય તો $'x'=.......$View Solution
- 5$8\ cm$ બાજુવાળા ચોરસના શિરોબિંદુ પર વિદ્યુતભાર $\frac{{10}}{3} \times {10^{ - 9}}$ $C$ મૂકતાં કેન્દ્ર પર વોલ્ટેજ કેટલો થાય?View Solution
- 6$10\,m$ ત્રિજયા ધરાવતા વર્તુળના કેન્દ્ર પર $10$ યુનિટ વિદ્યુતભાર મૂકેલો છે. તો $1$ એકમ વિદ્યુતભારને વર્તુળના પરિઘ પર પરિભ્રમણ કરાવવા માટે ....... એકમ કાર્ય કરવું પડેView Solution
- 7$X$-અક્ષ પર વિદ્યુતભાર $Q$ અનુક્રમે $x = 1, 2, 4, 8…meter$ પર મૂકેલા છે,તો $x = 0$ પર વિદ્યુતક્ષેત્ર અને વિદ્યુતસ્થિતિમાન કેટલું થાય?View Solution
- 8એક $3\ \mu F$ કેપેસિટરને $300\, V$ ના સ્થિતિમાન સુધી વિદ્યુતભારીત કરેલ છે અને $2\ \mu F$ કેપેસિટરને $200\, V $ સુધી વિદ્યુતભારિત કરેલ છે. ત્યારે કેપેસિટરને અસમાન ધ્રુવીયતા ધરાવતી પ્લેટો સાથે સમાંતરમાં એકબીજા સાથે જોડવામાં આવે છે. જો પ્લેટો આ રીતે જોડેલી હોય, તો કેટલા ......$\mu C$ વિદ્યુતભારનો જથ્થો પસાર થતો હશે ?View Solution
- 9વિધાન $-1$ : સમસ્થિતિમાન પૃષ્ઠ પર વિજભારને એક સ્થાનથી બીજા સ્થાને લઈ જવા માટે કોઈ કાર્ય કરવું પડતું નથી.View Solution
વિધાન $-2$ : સમસ્થિતિમાન પૃષ્ઠ પર વિદ્યુતબળની રેખાઓ સપાટીને લંબ હોય છે.
- 10આપેલ તંત્રની કુલ વિદ્યુતસ્થિતિઊર્જા કેટલા .......$J$ થાય? ( $\frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\ N - {m^2}/{C^2})$View Solution