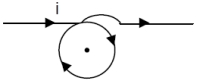
The magnetic field at \(B\) is given by,
\(\vec{B}_{ B }=\vec{B}_{\text {wire }}+\vec{B}_{\text {ring }}\)
\(=\left[\frac{\mu_{0} i}{2 r}(-\hat{k})+\frac{\mu_{0} i}{4 \pi r}(-\hat{k})\right]+\left[\frac{\mu_{0} i}{2 \pi r}(-\hat{k})+\frac{\mu_{0} i}{2 r}(-\hat{k})\right]\)
\(=\frac{\mu_{0} i}{2 \pi r}(-\hat{k})+\left[\frac{\mu_{0} i}{2 \pi r}+\frac{\mu_{0} i}{2 r}\right](-\hat{k})\)
\(=\frac{\mu_{0} i}{2 r}\left[\frac{1}{\pi}+1\right]\) \(....(I)\)
Substitute \(4 \pi \times 10^{-7}\) for \(\mu_{0}, 2.5\) for \(i\) and \(5 \times 10^{-2}\) for \(r\) in equation \((I).\)
\(\vec{B}_{ B }=\frac{\left(4 \pi \times 10^{-7}\right) 2.5}{2\left(5 \times 10^{-2}\right)}\left[\frac{1}{\pi}+1\right]\)
\(=10 \pi \times 10^{-6}\left[\frac{1}{\pi}+1\right]\)
\(=\pi \times\left[\frac{1}{\pi}+1\right] \times 10^{-5} T\)
Download our appand get started for free
Similar Questions
- 1સમાન ગતિઊર્જા ધરાવતો એક પ્રોટોન અને એક ડ્યુટેરોન $(q=+e, m=2.0 \mathrm{u})$ નિયમિત ચુંબકીય ક્ષેત્ર $\vec{B}$ માં $\vec{B}$ ને લંબરૂપે ગતિ $ક$ રે છે. ડ્યુટૅરેનનાં ગતિપથની ત્રિજ્યા $r_d$ અને પ્રોટોનમાં પથની ત્રિજ્યા $r_p$ નો ગુણોત્તર .......... છે.View Solution
- 2એકી-આયનીકૃત મેગ્નેશીયમ પરમાણુ $( A=24)$ ને $5 \,keV$ ની ગતિઊર્જ જેટલો પ્રવેગિત કરવામાં આવે છે, અને $0.5 \,T$ મૂલ્ય ધરાવતા યુંબકીકીય ક્ષેત્ર $B$ માં લંબરૂપે પ્રક્ષિપ્ત (ફેંકવામા) આવે છે. ગતિપથની ત્રિજ્યા .............. $cm$ થશે.View Solution
- 3$0.049 \mathrm{~T}$ જેટલા સમાન ચુંબકીય ક્ષેત્રમાં, એક ચુંબકીય સોય આકૃતિમાં દર્શાવ્યા પ્રમાણે $5$ સેકન્ડમાં $20$ પૂર્ણ દોલનો કરે છે. સોયની જડત્વની ચાકમાત્રા $9.8 \times 10^{-6} \mathrm{~kg} \mathrm{~m}^2$છે. જો સોયની સુંબકીય ચાકમાત્રા $x \times 10^{-5} \mathrm{Am}^2$ હોય તો ' $x$ ' નું મૂલ્ય. . . . . . . .થશે.View Solution
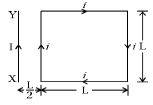
- 4એક ચોરસ લૂપ $ABCD$ માંથી $i $ પ્રવાહ પસાર થાય છે, તેને $I$ પ્રવાહધારીત રેખીય વાહકતાર $XY$ ની નજીક મૂકેલ છે, લૂપ પર પરિણામી બળ કેટલું લાગશે?View Solution
- 5$5\,cm,12\,cm$ અને $13\,cm$ બાજુઓ ધરાવતી કાટકોણ ત્રિકોણાકારની એક આંટાની પ્રવાહલૂપ $2\,A$ નો પ્રવાહ ધારણ કરે છે. આ લૂપ $0.75\,T$ મૂલ્ચના સમાન ચુંબકીયક્ષેત્રમાં લૂપની $13\,cm$ વાળી બાજુની સમાંતર દિશામાં મૂકવામાં આવે છે. $5\,cm$ ની બાજુ પર ચુંબકીય બળનું મૂલ્ય $\frac{x}{130}\,N$ છે. તો $x$ નું મૂલ્ય $...........$ છે.View Solution
- 6$L$ લંબાઇ અને $I$ પ્રવાહધારિત તારને વર્તુળમાં વાળતાં ચુંબકીય મોમેન્ટ કેટલું થાય?View Solution
- 7$120\,\Omega $ અવરોધવાળા ગેલ્વેનોમીટર સાથે $1\,\Omega $ નો શંટ અવરોધ જોડેલો છે. $5.5\, ampere$ પ્રવાહ માટે ગેલ્વેનોમીટર પૂર્ણ આવર્તન દર્શાવે છે. જો શંટ અવરોધ જોડેલો ન હોય તો ગેલ્વેનોમીટર પૂર્ણ આવર્તન વખતે કેટલા .............. $A$ નો પ્રવાહ દર્શાવશે?View Solution
- 8View Solutionનીચેનામાંથી ક્યું વાક્ય મુજબ ચુંબકીય બળ રેખાનાં સંદર્ભે સાચી છે ?
- 9$2\,\mu C$ વિજભાર ધરાવતો કણ $y-$દિશામાં $2\, T$ જેટલા ચુંબકીયક્ષેત્રમાં $\left( {2\hat i + 3\hat j} \right) \times {10^6}\,m{s^{ - 1}}$ ના વેગથી ગતિ કરતો હોય તો તેના પર કેટલું ચુંબકીય બળ લાગતું હશે?View Solution
- 10$10 \Omega$ ગૂંચળાનો અવરોધ ધરાવતું ગેલ્વેનોમીટર $3 m A$ પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન દર્શાવે છે. તેના વડે $8 A$ પ્રવાહ માપવા માટે શટ અવરોધ કેટલો હોવો જોઈએ?View Solution
