અચળ દબાણે ત્રિપરમાણ્વિક, દ્વિપરમાણ્વિક અને એેક પરમાણ્વિક વાયુને ઉષ્માનો એેકસમાન જથ્થો આપવામાં આવતુ હોય તો...
Medium
Download our app for free and get started
c
(c)
(c)
\(\frac{\Delta U}{\Delta Q}=\frac{n C_V \Delta T}{n C_P \Delta T}=\frac{C_V}{C_P}=\frac{1}{\gamma}\)
\(\left(\frac{\Delta U}{\Delta Q}\right)_{\text {mono }}=\frac{1}{\gamma_{\text {mono }}}=\frac{3}{5}\)
\(\left(\frac{\Delta U}{\Delta Q}\right)_{\text {dia }}=\frac{1}{\gamma_{\text {dia }}}=\frac{5}{7}\)
\(\left(\frac{\Delta U}{\Delta Q}\right)_{\text {tria }}=\frac{1}{\gamma_{\text {tria }}}=\frac{3}{4}\)
Fractional energy used to change internal energy is maximum in Triatomic gas.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionબહુપરમાણ્વિક પ્રક્રિયામાં વાયુની વિશિષ્ટ ઉષ્મા ધારિતા શેના વડે આપવામાં આવે છે ?
- 2$16\,g$ હીલિયમ વાયુ અને $16\,g$ ઑક્સીજનનું મિશ્રણ કરવામાં આવે તો મિશ્રણ માટે $\frac{{{C_P}}}{{{C_V}}}$ નો ગુણોત્તર કેટલો થાય?View Solution
- 3વાયુનું તાપમાન $-73°C$ છે. ........ $^oC$ તાપમાને વાયુને ગરમ કરવો જોઈએ જેથી પરમાણુઓની $rms$ વેગ બમણો થાય $?$View Solution
- 4$P$ અવસ્થામાં રહેલા વાયુ $a$ માટે $C_{p}-C_{V}=R$ અને $Q$ અવસ્થામાં $C_{p}-C_{V}=1.10 R$, $T_{p}$ અને $T_{Q}$ એ અનુક્રમે બે જુદી અવસ્થા $P$ અને $Q$ ના તાપમાન હોય, તોView Solution
- 5View Solutionઅચળ દબાણે ત્રિપરમાણ્વિક, દ્વિપરમાણ્વિક અને એેક પરમાણ્વિક વાયુને ઉષ્માનો એેકસમાન જથ્થો આપવામાં આવતુ હોય તો...
- 6$T$ તાપમાને આદર્શ દ્વિ આણ્વિય વાયુની $rms$ ઝડપ $v$ છે. જ્યારે વાયુ પરમાણુઓમાં વિભાજીત થાય ત્યારે તેની નવી $rms$ ઝડપ બમણી થાય છે. કયા તાપમાને વાયુનું વિભાજન થાય છે $?$View Solution
- 7${N}_{2}$ વાયુના અણુંની કયા તાપમાને ગતિઊર્જા $0.1\;volt$ થી પ્રવેગિત કરેલા સ્થિર ઇલેક્ટ્રોનની ગતિઊર્જા જેટલી થાય? (નજીકના પૂર્ણાંકમાં)View Solution
$\left(\right.\left.{k}_{{B}}=1.38 \times 10^{-23} \, {J} / {K}\right)$
- 8વિધાન : એક પરમાણ્વિક વાયુ માટે $\frac{C_p}{C_v}$ નો ગુણોત્તર દ્વિ પરમાણ્વિક વાયુના $\frac{C_p}{C_v}$ ના ગુણોત્તર કરતાં ઓછો હોયView Solution
કારણ : એક પરમાણ્વિક વાયુ માટેના મુક્તતાના અંશો દ્વિ પરમાણ્વિક વાયુના મુક્તતાના અંશો કરતાં ઓછા હોય
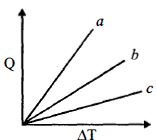
- 9એક પરમાણ્વિક $(M)$, દ્વિ પરમાણ્વિક $(D)$ અને બહુ પરમાણ્વિક $(P)$ વાયુઓની સમદાબી પ્રક્રિયા માટે આપેલી ઉષ્મા$(Q)$ અને તાપમાનના થતાં ફેરફાર$\left( {\Delta T} \right)$ વચ્ચેનો ગ્રાફ આપેલ છે.શરૂઆતમાં બધા જ વાયુ સમાન છે જો કંપનગતિ માટે મુક્તતાના અંશોને અવગણવામાં આવે તો $a, b$ અને $c$ ગ્રાફની રેખા કોને અનુરૂપ હશે?View Solution
- 10$27^{\circ} C$ તાપમાને અને $1$ વાતાવરણ દબાણે રહેલા વાયુ માટે આપેલા દળ ધરાવતા અણુઓની સરેરાશ વર્ગિત વર્ગમૂળ $(r.m.s.)$ ઝડપ $200\, ms ^{-1}$ છે. $127^{\circ} C$ તાપમાને અને $2$ વાતાવરણ દબાણે રહેલા વાયુ માટે અણુઓની સરેરાશ વર્ગિત વર્ગમૂળ ઝડપ $\frac{ x }{\sqrt{3}}\, ms ^{-1}$ છે. $x$ નું મૂલ્ય ......... $ms ^{-1}$ હશે.View Solution