भूमि के एक बिंदु $P$ से एक $10 m$ ऊँचे भवन के शिखर का उन्नयन कोण $30^\circ$ है। भवन के शिखर पर एक ध्वज को लहराया गया है और $P$ से ध्वज के शिखर का उन्नयन कोण $45^\circ$ है। ध्वजदंड की लंबाई और बिंदु $P$ से भवन की दूरी ज्ञात कीजिए। $($ यहाँ आप $\sqrt{3} = 1.732$ ले सकते हैं।$)$
example-4
Download our app for free and get started
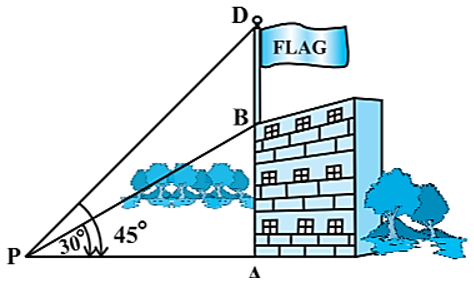
आकृति में, $AB$ भवन की ऊँचाई प्रकट करता है, $BD$ ध्वजदंड प्रकट करता है और $P$ दिया हुआ बिंदु प्रकट करता है। ध्यान दीजिए कि यहाँ दो समकोण त्रिभुज $ \text{PAB}$ और $\text{PAD}$ हैं। हमें ध्वजदंड की लंबाई अर्थात् $DB$ और बिंदु $P$ से भवन की दूरी अर्थात् $PA$ ज्ञात करना है।
क्योंकि हमें भवन की ऊँचाई $AB$ ज्ञात है इसलिए पहले हम समकोण $\triangle \text{PAB}$ लेंगे।
यहाँ $\tan 30^\circ = \frac{\mathrm{AB}}{\mathrm{AP}}$
अर्थात् $\frac{1}{\sqrt{3}}=\frac{10}{\mathrm{AP}}$
इसलिए $AP = 10 \sqrt{3}$
अर्थात् $P$ से भवन की दूरी $10\sqrt{3} m = 17.32 m$
आइए अब हम यह मान लें कि $DB = x m$ है तब $AD = (10 + x)m$
अब समकोण $\triangle \text{PAD}$ में $\tan 45^\circ = \frac{\mathrm{AD}}{\mathrm{AP}}=\frac{10+x}{10 \sqrt{3}}$
इसलिए $1 = \frac{10+x}{10 \sqrt{3}}$
अर्थात् $x = 10 (\sqrt{3} - 1) = 7.32$
अतः ध्वजदंड की लंबाई $7.32 m$ है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1एक बहुमंजिल भवन के शिखर से देखने पर एक $8 m$ ऊँचे भवन के शिखर और तल के अवनमन-कोण क्रमशः $30^\circ$ और $45^\circ$ हैं। बहुमंजिल भवन की ऊँचाई और दो भवनों के बीच की दूरी ज्ञात कीजिए।View Solution
- 2$1.5 m$ लंबा एक प्रेक्षक एक चिमनी से $28.5 m$ की दूरी पर है। उसकी आँखों से चिमनी के शिखर का उन्नयन कोण $45^\circ$ है। चिमनी की ऊँचाई बताइए।View Solution
- 3एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में $40 m$ अधिक लंबी हो जाती है जबकि सूर्य का उन्नतांश $($altitude$) 60^\circ$ से घटकर $30^\circ$ हो जाता है अर्थात् छाया के एक सिरे से मीनार के शिखर का उन्नयन कोण $60^\circ$ है और $DB$ छाया की लंबाई है जबकि उन्नयन कोण $30^\circ$ है। मीनार की ऊँचाई ज्ञात कीजिए।View Solution
- 4धरती पर एक मीनार ऊध्ध्वाधर खड़ी है। धरती के एक बिंदु से, जो मीनार के पाद$-$बिंदु से $15 m$ दूर है, मीनार के शिखर का उन्नयन कोण $60^\circ$ है। मीनार की ऊँचाई ज्ञात कीजिए।View Solution
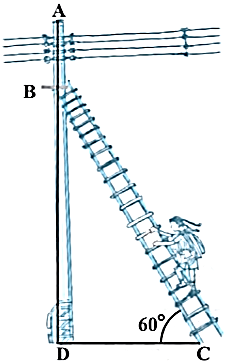
- 5एक बिजली मिस्त्री को एक $5 m$ ऊँचे खंभे पर आ गई खराबी की मरम्मत करनी है। मरम्मत का काम करने के लिए उसे खंभे के शिखर से $1.3 m$ नीचे एक बिंदु तक वह पहुँचना चाहती है $($देखिए आकृति$)।$ यहाँ तक पहुँचने के लिए प्रयुक्त सीढ़ी की लंबाई कितनी होनी चाहिए जिससे कि क्षैतिज से $60^\circ$ के कोण से झुकाने पर वह अपेक्षित स्थिति तक पहुँच जाए? और यह भी बताइए कि खंभे का पार$-$बिंदु कितनी दूरी पर सीढ़ी के पार$-$बिंदु से होना चाहिए? $($यहाँ आप $\sqrt{3} = 1.73$ ले सकते हैं$।)$View Solution
- 6एक नदी के पुल के एक बिंदु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः $30^\circ$ और $45^\circ$ हैं। यदि पुल किनारों से $3 m$ की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात कीजिए।View Solution