दिये गये चित्र में यदि चुम्बकीय फ्लक्स परिवर्तन कराया जाए $V$ वोल्ट का वि.वा. बल बनता है। एक आवेश $Q$ को लूप पर घुमाने में किया गया कार्य है :
[2005]
Download our app for free and get started
(a) दक्षता $E =\frac{ W }{ Q }$
$ \Rightarrow V =\frac{ W }{ Q } \Rightarrow W = QV $
$ \Rightarrow V =\frac{ W }{ Q } \Rightarrow W = QV $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1दो कुण्डलियों का अन्तः प्रेरण $0.005 H$ है। पहली कुण्डली में धारा $I = I _0 \sin \omega t$ से परिवर्तित होती है जहां $I _0=10 A$ तथा $\omega=100 \pi$ रेडियन/सेकंड तो उच्चतम वि. वा.ब. :View Solution
- 2एक स्वप्रेरण $L =2 mH$ में धारा $i = t ^2 e ^{- t }$ से परिवर्तित होता है। किस समय वि.वा.ब. का मान शून्य होगा:View Solution
- 3एक चालक वृत्तीय फंद को $0.04 T$ के अचर चुम्बकीय क्षेत्र में इस तरह रखा है कि फंद का तल चुम्बकीय क्षेत्र की दिशा से लम्ब दिशा में है। फन्द् की त्रिज्या $2 mm / s$. की दर से घटने लगती है। जब फन्द की त्रिज्या $2 cm$ होगी तो इसमें प्रेरित वि.वा.ब. $( emf )$ का मान होगा:-View Solution
- 4एक आयताकार, एक वर्गाकार, एक वृत्तीय और एक दीर्घवृत्तीय फन्द जो सभी $x - y$ तल में हैं, एक अचर चुम्बकीय क्षेत्र से स्थिर वेग $\overrightarrow{ V }= v \hat{ i }$ से बाहर निकल रहे हैं। चुम्बकीय क्षेत्र की दिशा ऋणात्मक $z$ अक्ष की दिशा में है। क्षेत्र से बाहर निकलने के प्रक्रम में इन फन्दों में प्रेरित वि.वा.ब (emf) स्थिरमानी नहीं रहेगा :-View Solution
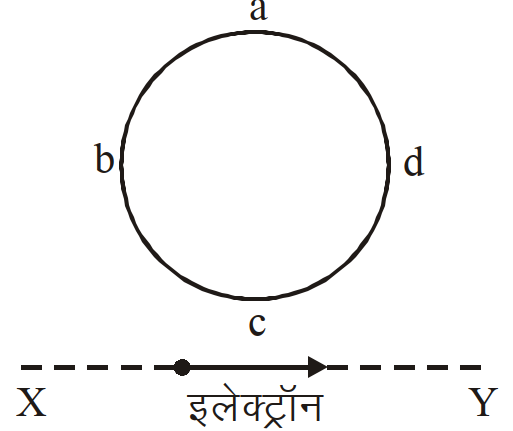
- 5एक इलेक्ट्रॉन सरल रेखीय पथ, $XY$ पर गतिमान है। एक कुंडली abcd इस इलेक्ट्रॉन के मार्ग के निकटवर्ती है (आरेख देखिये) तो, इस कुंडली में प्रेरित धारा (यदि कोई हो तो) की दिशा क्या होगी?View Solution
- 6एक $0.4$ मी लम्बाई वाला चालक $7$ मी/सेकण्ड से चुम्बकीय क्षेत्र $B =0.9$ वेबर $/$ मी $^2$ के लम्बवत् घूमता है। इसमें प्रेरक वि.वा.ब. होगा :View Solution
- 7एक लम्बे बहुकुंडलक(सोलिनाइड) में 500 फेरें हैं। जब इसमें 2 ऐम्पीयर की धारा प्रवाहित की जाती है, तो हर फेरे से सम्बन्धित चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ होती है। सोलिनाइड का स्वप्रेरकत्व होगा:View Solution
- 8एक कुण्डली में फरों की संख्या $N$ है तो स्व-प्रेरण गुणांक किसके समानुपाती होगा?View Solution
- 9एक कुण्डली जिसमें 50 फेरे हैं एक चुम्बकीय क्षेत्र $2 \times$ $10^{-2} T$ के लम्बवत् रखी जाती है। कुण्डली का क्षेत्रफल 100 सेमी $^2$ है। इसमे उत्पन्न प्रेरक वि.वा.ब. $0.1 V$ है। कुण्डली को 1 सेकण्ड में चुम्बकीय क्षेत्र से हटा दिया जाता है तो $t$ का मान हैView Solution
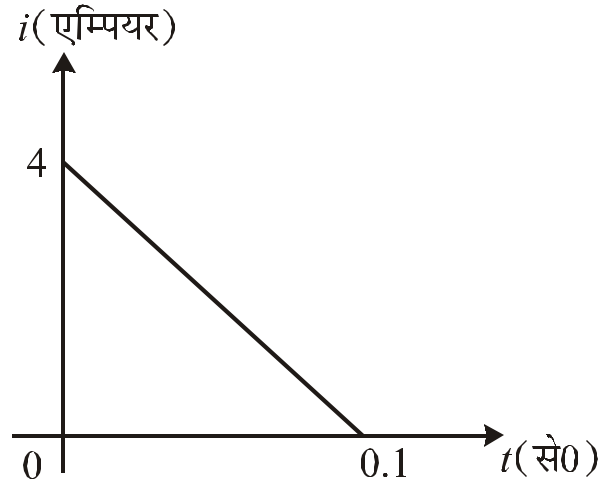
- 10$10 \Omega$ प्रतिरोध की एक कुंडली में, इससे संबद्व चुम्बकीय फ्लक्स के परिवर्तन से प्रेरित विधुत धारा को समय के फलन के रूप में दिये गए आरेख द्वारा प्रदर्शित किया गया है तो, इस कुंडली से संबद्व फ्लक्स में परिवर्तन का मान वेबर में है:View Solution
