एक $m$ द्रव्यमान का पिण्ड ऊर्ध्वाधरत सरल: आवर्तगति करता है। जब द्रव्यमान को स्प्रिंग $A$ से लटकाया जाता है तो उसका आवर्तकाल $t_1$ तथा $B$ से लटकाने पर आवर्तकाल $t _2$ है। यदि $A$ तथा $B$ को दिये गये चित्र की तरह जोड़ा जाए तो आवर्तकाल $t _0$ दिया जाता है
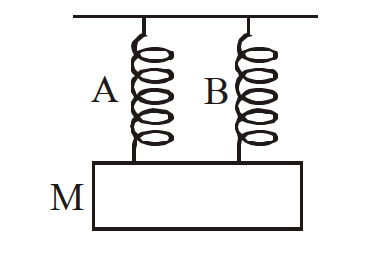
[2002]
Download our app for free and get started
(d) $t =2 \pi \sqrt{\frac{ m }{ k }} \Rightarrow k \propto t ^{-2}$
यदि स्प्रिंग समांतर में जोड़े जाए तो $k _0= k _1+ k _2$ जहाँ $k _0$ परिणामी स्प्रिंग-नियतांक $t _0^{-2}= t _1^{-2}+ t _2^{-2}$
यदि स्प्रिंग समांतर में जोड़े जाए तो $k _0= k _1+ k _2$ जहाँ $k _0$ परिणामी स्प्रिंग-नियतांक $t _0^{-2}= t _1^{-2}+ t _2^{-2}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1दो कण, एक दूसरे के निकट स्थित, दो समान्तर सरल रेखाओं के अनुदिश, समान आवृति और आयाम से दोलन कर रहे हैं। जब उनका विस्थापन उनके आयाम का आधा $(1 / 2)$ होता है तो वे एक दूसरे से विपरीत दिशा में गति कर रहे होते हैं। दोनों कणों की माध्य स्थिति, उनके मार्गों की लम्बवत् एक सरल रेखा पर स्थित है। तो कलान्तर है :View Solution
- 2एक पिण्ड सरल आवर्तगति करता है। जब उसका विस्थापन माध्य स्थिति से $4$ सेमी तथा $5$ सेमी हो तो उसका वेग $10$ सेमी/सेकंड तथा $8$ सेमी/सेकंड है, इसका आवर्तकाल होगा $-$View Solution
- 3View Solutionएक सरल लोलक में एक धातु का लोलक इस्तेमाल किया गया है जो ऋणावेशित है। यह एक धनावेशित प्लेट के ऊपर दोलन करता है। तो इसका आवर्तकाल
- 4एक कण का द्रव्यमान $m$ है। इसे विराम अवस्था से मोचित किया गया है और यह आरेख मे दिखाये गये अनुसार एक परवलीय मार्ग पर चलता है। यह मानते हुए कि कण का मूल स्थिति से विस्थापन कम है, कौन से ग्राफ कण की स्थिति को समय के फलन के रूप में सही दर्शाता है?View Solution
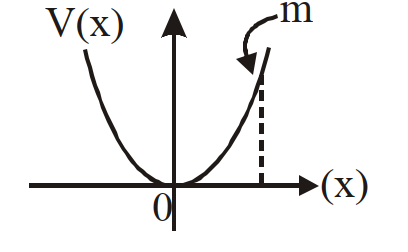
- 5द्रव्यमान $m$ का एक कण दो बिन्दुओं $x _1$ व $x _2$ के बीच सरल आवर्त गति में कम्पन करता है, साम्य स्थिति $O$ है, तो इसकी स्थितिज ऊर्जा का ग्राफ होगा:View Solution
- 6एक कण आयाम $A$ के साथ सरल आवर्तगति करता है। माध्य स्थिति से कितनी दूरी पर उसकी स्थितिज ऊर्जा कुल ऊर्जा की एक चौथाई है ?View Solution
- 7एक सरल आवृर्त्त दोलनचित्र में बल नियतांक $2 \times 10^6$ न्यूटन/मीटर, आयाम $0.01$ मीटर तथा कुल ऊर्जा $160 J$ है; तोView Solution
- 8एक कण सरल आवर्ती गति में है। इसके तात्क्षणिक वेग और त्वरण का कलान्तर होगा $-$View Solution
- 9एक ऊर्ध्व दिशा की कमानी को धरातल पर चित्र के अनुसार स्थायी किया गया है तथा इसके ऊपरी सिरे के पलड़े पर $2.0$ किग्रा द्रव्यमान की वस्तु रखी है। कमानी और पलड़े के भार नगण्य हैं। थोड़ा दबाकर छोड़ देने पर द्रव्यमान सरल आवर्ती गति करता है। कमानी का बल नियतांक 200 न्यूटन/मी है। आवर्त गति का न्यूनतम आयाम कितना होना चाहिए, जिससे ऊपर रखी वस्तु पलड़े से अलग हो जाये?( मान लो $g =10$ मी $/$ से $^2$ )View Solution
- 10$5$ सेमी आयाम की सरल आवर्त गति करते एक कण की अधिकतम चाल $31.4$ सेमी./से है। इसके कम्पन की आवृत्ति हैView Solution