$i-\delta $ આલેખ પરથી પ્રિઝમના કાંચનો વક્રિભવનાંક શોધવાના પ્રયોગમાં એમ જોવા મળયું કે $35^o $ ના ખૂણે આપાત થતું કિરણ $40^o $ નું વિચલન પામે છે,અને તે $79^o $ ના ખૂણે નિર્ગમન પામે છે.આ કિસ્સામાં નિમ્ન આપેલ મૂલ્યોમાંથી સૌથી નજીકનો વક્રિભવનાંક થશે.
JEE MAIN 2016, Medium
c
We know that \(i+e-A=\delta\)
We know that \(i+e-A=\delta\)
\(35^o+79^o-\mathrm{A}=40^o\) \(\therefore \quad \mathrm{A}=74^o\)
But \(\mu = \frac{{\sin \left( {\frac{{{\text{A}} + {\delta _{\text{m}}}}}{2}} \right)}}{{\sin {\text{A}}/2}}\) \( = \frac{{\sin \left( {\frac{{74 + {\delta _{\text{m}}}}}{2}} \right)}}{{\sin \frac{{74}}{2}}}\)
\( = \frac{5}{3}\sin \left( {{{37}^o} + \frac{{{\delta _{\text{m}}}}}{2}} \right)\)
\(\mu_{\max }\) can be \(\frac{5}{3}\). That is \(\mu_{\max }\) is less than \(\frac{5}{3}=1.67\)
But \(\delta_{\mathrm{m}}\) will be less than \(40^o\) so
\(\mu < \frac{5}{3}\sin {57^o}\) \( < \frac{5}{3}\sin {60^o}\) \( \Rightarrow \mu = 1.45\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$3/2$ વક્રીભવનાંક ધરાવતાં બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ $0.3\,\, m$ જેટલી છે. જો તેને $4/3$ વક્રીભવનાંક ધરાવતાં પાણીમાં ડૂબાડવામાં આવે ત્યારે લેન્સની કેન્દ્રલંબાઈ.......$cm$ માં શોધો.View Solution
- 2ઉદગમ $L$ માંથી કિરણ $x$ અંતરે રહેલા સમતલ અરીસા પર લંબ પડે છે. કિરણ સ્ત્રોત ઉદગમ $L$ ની બરાબર ઉપર મૂકવામાં આવેલા સ્કેલ પર બિંદુ તરીકે પાછું પ્રતિબિંબિત થાય છે. હવે અરીસાને $\theta $ ખૂણે ફેરવતા આ બિંદુ સ્કેલ પર ઉપર તરફ $y $ જેટલા અંતરે ખસે છે. $\theta$ શેના વડે આપી શકાય?View Solution
- 3સમબાજુ પ્રિઝમ માટે આપાતકોણ અને નિર્ગમનકોણ પ્રિઝમકોણથી $3/4$ ગણો છે.તો વિચલનકોણ કેટલા......$^o$ હશે?View Solution
- 4પાતળા કાચના (વક્રીભવનાંક $1.5$) લેન્સનો હવામાં ઓપ્ટિક્લ પાવર $-5 D$ તો $1.6$ વક્રીભવનાંક પ્રવાહીમાં તેનો ઓપ્ટિકલ પાવર .....થશે.View Solution
- 5સંયુક્ત માઇક્રોસ્કોપ માં ઓબ્જેક્ટિવ અને આઈપીસની કેન્દ્રલંબાઈ અનુક્રમે $1\,cm$ અને $5\,cm$ છે. તેમની વચ્ચેનું અંતર $10\,cm$ છે વસ્તુ અને ઓબ્જેક્ટિવ વચ્ચેનું અંતર $\frac{ n }{40}\, cm$ રાખવાથી આંખ પર તણાવ લઘુતમ થાય તો $n=$.............View Solution
- 6બહિર્ગોળ લેન્સના એક પ્રયોગમાં, પ્રતિબિંબ અંતર $(v')$ વિરુદ્ધ કેન્દ્રથી મપાયેલ વસ્તુ અંતર $(\mu ')$ માટે $v'\mu '=225$ આપે છે. જો બધા જ અંતરો $cm$ એકમમાં માપતા હોય તો લેન્સની કેન્દ્રલંબાઈનું મૂલ્ય $...........cm$ થશે.View Solution
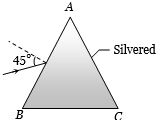
- 7$30^o $ પ્રિઝમકોણ માટે $45^o $ આપાતકોણ છે.કિરણ $AC$ દ્વારા પરાવર્તન થઇને મૂળ માર્ગે પાછો ફરે છે. તો પ્રિઝમનો વક્રીભવનાંક કેટલો હશે?View Solution
- 8ટેલિસ્કોપનો મેગ્નિફિકેશન પાવર $9$ અને લેન્સ વચ્ચેનું અંતર $20\, cm$ છે તો ઘટક લેન્સની કેન્દ્રલંબાઈ શું થશે?View Solution
- 9$10^o$ પ્રિઝમકોણ $(n=1.602)$ પ્રિઝમ એ બીજા પ્રિઝમ $(n=1.500)$ સાથે ગોઠવતા કિરણ વિચલન અનુભવતો નથી તો બીજા પ્રિઝમનો પ્રિઝમકોણ કેટલો થાય?View Solution
- 10જો એસ્ટ્રોનોમિકલ ટેલિસ્કોપની ટ્યૂબની $105\, cm$ અને મેગ્નેફિકેશન પાવર સામાન્ય ગોઠવણ માટે $20 $ હોય તો તેની ઓબ્જેક્ટિવ લેન્સની કેન્દ્રલંબાઈ.......$cm$ થશે?View Solution
