If the charge on an electron is $1.6 \times 10$ coulombs, how many electrons should pass through a conductor in $1$ second to constitute $1$ ampere current?
We know that
$\text{I}=\frac{\text{Q}}{\text{T}}$
$\Rightarrow1\text{A}=\frac{\text{Q}}{1\text{s}}$
$\Rightarrow\text{Q}=1\text{C}$
Now, when charge is $1.6 \times 10^{-19}$ Coulamb, number of electrone $= 1$
When charge is $1$ Coulamb, number of electrone $=\frac{1}{1.6\times10^{-19}}=0.625\times10^{19}=625\times10^{18}$
$\text{I}=\frac{\text{Q}}{\text{T}}$
$\Rightarrow1\text{A}=\frac{\text{Q}}{1\text{s}}$
$\Rightarrow\text{Q}=1\text{C}$
Now, when charge is $1.6 \times 10^{-19}$ Coulamb, number of electrone $= 1$
When charge is $1$ Coulamb, number of electrone $=\frac{1}{1.6\times10^{-19}}=0.625\times10^{19}=625\times10^{18}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1A p.d. of 6V is applied to two resistors of $3 Ω$ and $6 Ω$ connected in parallel. Calculate:View Solution
The combined resistance.
The current flowing in the main circuit.
The current flowing in the $3 Ω$ resistor. - 2For the circuit shown in the diagram below:View Solution
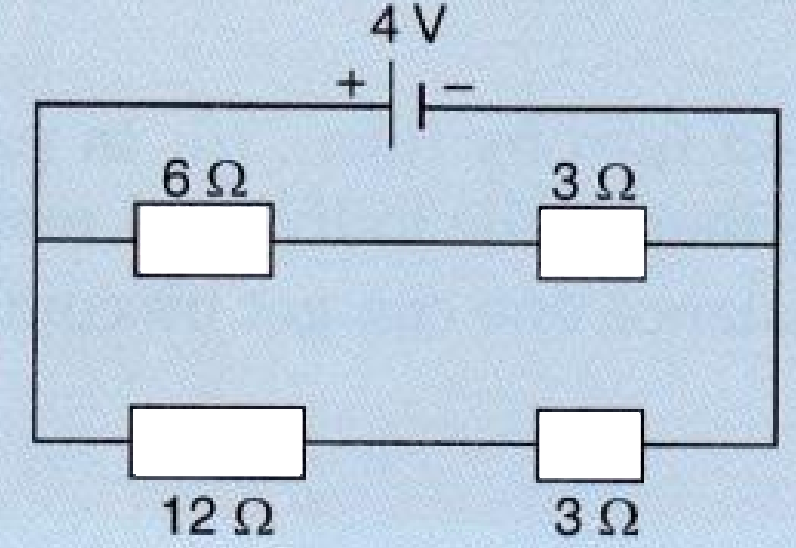
What is the value of :
Current through $6 Ω$ resistor?
Potential difference across $12 Ω$ resistor? - 3A wire is 1.0m long, 0.2mm in diameter and has a resistance of $10Ω.$ Calculate the resistivity of its material?View Solution
- 4View SolutionHow does the resistance of a conductor depend on:
- Length of the conductor?
- Area of cross-section of the conductor?
- Temperature of the conductor?
- 5What will be the resistance of a metal wire of length $2$ metres and area of cross-section $1.55 \times 10m $, if the resistivity of the metal be $2.8 \times 10 m?$View Solution
- 6View SolutionDraw circuit symbols for:
- Fixed resistance.
- Variable resistance.
- A cell.
- A battery of three cells.
- An open switch.
- A closed switch.
- 7The electrical resistivities of four materials $A, B, C$ and $D$ are given below:View Solution
$\text{A}\ -110\times10^{-8}\Omega\text{ m}$
$\text{B}-\ 1.0\times10^{10}\Omega\text{ m}$
$\text{C}-\ 10.0\times10^{-8}\Omega\text{ m}$
$\text{D}-\ 2.3\times10^{3}\Omega\text{ m}$
Which material is:- Good conductor.
- Resistor.
- Insulator, and
- Semiconductor
- 8Calculate the resistance of an aluminium cable of length $10\ km$ and diameter $2.0\ mm$ if the resistivity of aluminium is $2.7\times10 Ω\ \text{m}.$View Solution
- 9A piece of wire of resistance $20 Ω$ is drawn out so that its length is increased to twice its original length. Calculate the resistance of the wire in the new situation.View Solution
- 10How will you connect three resistors of resistances $2Ω, 3Ω$ and $6Ω $ obtain a total n si stance of:View Solution
- $4 Ω,$
- $1Ω$
