જો $B$ ની સાંદ્રતા બમણી કરવામાં આવે તો બે પ્રક્રિયક $A$ અને $B$ વચ્ચેની પ્રક્રિયાનો વેગ $4$ ના ગુણકથી ઘટે છે. તો પ્રક્રિયક $B$ ના સંદર્ભમાં આ પ્રક્રિયાનો ક્રમ ............ થશે.
AIPMT 2005, Diffcult
Download our app for free and get started
b
$R = k\,{[B]^n}$;
$R = k\,{[B]^n}$;
$\frac{1}{4}R = k{[2B]^n}$;
$4 = {\left( {\frac{1}{2}} \right)^n}$;
$4 = {2^{ - n}}$;
$n = - 2$.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1શૂન્ય ક્રમતી એક પ્રક્રિયાતો વેગ અચળાંક $2.0\times10^{-2}\, mol\, L^{-1}\, s^{-1}$ છે. જો $25\, seconds$ પછી પ્રક્રિયાની સાંદ્રતા $0.5\, M$ હોય તો શરૂઆતની સાંદ્રતા ......... $M$ માં શું હશે ?View Solution
- 2પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે જ્યારે $\log \,k$ વિરૂદ્ધ $1/T $ નો આલેખ આપેલ છે. જેનો ઢાળ $-8000 $ સીધી રેખામાં મળે છે,તો પ્રક્રિયાની સક્રીયકરણ ઊર્જા ......... $cal$ શોધો.View Solution
- 3પ્રથમક્રમની એક પ્રક્રિયામાં પ્રક્રિયક $ X $ ની સાંદ્રતા $ 0.1\,M$ થી ઘટીને $0.005\,M $ થવા માટે $40$ મિનિટ લાગે છે. જ્યારે $ X $ ની સાંદ્રતા $0.01\,M$ હોય, ત્યારે પ્રક્રિયાવેગનું મૂલ્ય કેટલું હશે ?View Solution
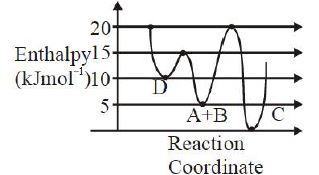
- 4$A$ અને $B$ વચ્ચેની નીચેની પ્રક્રિયાની એન્થાલ્પીનો આપેલ આલેખ ધ્યાનમાં લો. $A + B \to C + D$View Solution
ખોટું વિધાન ઓળખો.
- 5$30^{\circ} C$ પર, $AB _2$ ના વિધટનનો અર્ધ આયુષ્ય $200 \,s$ છે અને જે $AB _2$ ના પ્રારંભિક સાંદ્રતાથી સ્વતંત્ર છે. તો $80\, \% AB _2$ ના વિઘટન માટેના સમયની સીમા શોધો. ($s$ માં)View Solution
(આપેલ : $\log 2=0.30, \log 3=0.48$ )
- 6ધારીલો કે, $1\,\mu\,g$ ઓછા પ્રમાણમાં રેડિયો એકિટવ તત્ત્વ $ X$ કે જેનું અર્ધ આાયુષ્ય $30$ વર્ષ છે,જે ઉગતા વૃક્ષમાં અવશોષણ પામે છે. તો $100$ વર્ષ બાદ $X$ની માત્રા જે વૃક્ષમાં રહેશે તે $......\times 10^{-1}\,\mu\,g$ માં શોધો.[આપેલ: $\ln 10=2.303 ; \log 2=0.30]$View Solution
- 7પ્રક્રિયા :View Solution
$C{l_{2(aq)}} + {H_2}{S_{(aq)}} \to {S_{(S)}} + 2H_{(aq)}^ + + 2Cl_{(aq)}^ - $ માટે વેગ $= K[Cl_2][H_2S]$ છે તો કયો તબક્કો વેગ સમીકરણ સાથે સુસંગત છે ?
$(A)$ $Cl_2 + H_2S \rightarrow H^++ Cl^- + Cl^+ + HS^-$ (ધીમો); $ Cl^+ + HS^- \rightarrow H^++ Cl^- + S$ (ઝડપી)
$ (B)$ $H_2S $ $\rightleftharpoons$ $ H^+ + HS^-$ (ઝડપી સંતુલન) ; $Cl_2 + HS^- \rightarrow 2Cl^- + H^+ + S $ (ધીમો)
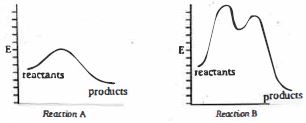
- 8View Solutionનીચેની બે પ્રક્રિયાઓ માટે, કયુ વિધાન સાચું છે?
- 9View Solutionજો સાંદ્રતા મોલ/લિટરમાં દર્શાવવામાં આવે તો પ્રથમક્રમની પ્રક્રિયા માટે વેગ અચળાંકનો એકમ........ છે.
- 10એસિડ દ્રાવણમાં થતા એસિટોનના બ્રોમીનેશનને નીચેના સમીકરણ વડે દર્શાવાય છે.View Solution
$CH_3COCH_{3(aq)} + Br_{2(aq)} \rightarrow $$CH_3COCH_2Br_{(aq)} + H^+_{(aq)}+ Br^-_{(aq)}$
નીચેની પ્રક્રિયા સાંદ્રતા પરથી આ ગતિકીય માહિતી મળે છે.
શરૂઆતની સાંદ્રતા, $M$
$[CH_3COCH_3]$ $[Br_2]$ $[H^+]$ $0.30$ $0.05$ $0.05$ $0.30$ $0.10$ $0.05$ $0.30$ $0.10$ $0.10$ $0.40$ $0.05$ $0.20$ $Br_2$ ના દૂર થવાનો શરૂઆતનો દર $Ms^{-1}$ માં નીચે મુજબ છે.
$5.7 \times 10^{-5} ,$ $5.7 \times 10^{-5} ,$ $1.2 \times 10^{-5} ,$ $3.1 \times 10^{-5}$
આ માહિતીને આધારે વેગ સમીકરણ ...... થશે.