$n$ સમાન ઘનાકાર ટુકડાઓ ની સેટ લીસ્સી સમક્ષિતિજ સપાટી પર રેખીય દિશામાં એકબીજાને સમાંતર રહે તેમ મૂકેલા છે. કોઈપણ બે નજીકના બ્લોકની સપાટીઓ વચ્ચે નું અંતર $L$ છે. એક છેડે રહેલા બ્લોક ને $t = 0$ સમયે $v$ ઝડપ થી તેની પછીના બ્લોક તરફ ગતિ કરવવામાં આવે છે. દરેક સંઘાત સંપૂર્ણ રીતે સ્થિતિસ્થાપક છે. તો.....
IIT 1995, Diffcult
b
(b,d)Since collision is perfectly inelastic so all the blocks will stick together one by one and move in a form of combined mass.
Time required to cover a distance \(‘L’\) by first block \( = \frac{L}{v}\)
Now first and second block will stick together and move with \(v/2 \) velocity (by applying conservation of momentum) and combined system will take time \(\frac{L}{{v/2}} = \frac{{2L}}{v}\) to reach up to block third.
Now these three blocks will move with velocity \(v/3 \) and combined system will take time \(\frac{L}{{v/3}} = \frac{{3L}}{v}\) to reach upto the block fourth.
So, total time \( = \frac{L}{v} + \frac{{2L}}{v} + \frac{{3L}}{v} + ...\frac{{(n - 1)L}}{v}\)\( = \frac{{n(n - 1)L}}{{2v}}\)
and velocity of combined system having \(n\) blocks as \(\frac{v}{n}\).
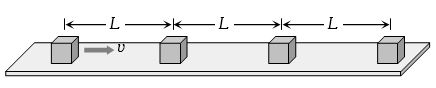
(b,d)Since collision is perfectly inelastic so all the blocks will stick together one by one and move in a form of combined mass.
Time required to cover a distance \(‘L’\) by first block \( = \frac{L}{v}\)
Now first and second block will stick together and move with \(v/2 \) velocity (by applying conservation of momentum) and combined system will take time \(\frac{L}{{v/2}} = \frac{{2L}}{v}\) to reach up to block third.
Now these three blocks will move with velocity \(v/3 \) and combined system will take time \(\frac{L}{{v/3}} = \frac{{3L}}{v}\) to reach upto the block fourth.
So, total time \( = \frac{L}{v} + \frac{{2L}}{v} + \frac{{3L}}{v} + ...\frac{{(n - 1)L}}{v}\)\( = \frac{{n(n - 1)L}}{{2v}}\)
and velocity of combined system having \(n\) blocks as \(\frac{v}{n}\).

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કોલમ $-I$ અને કોલમ $-II$ સાથે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ થયેલું કાર્ય શૂન્ય $(a)$ ગુરુત્વાકર્ષણ બળ વડે $(2)$ થયેલું કાર્ય ધન $(b)$ ગુરુત્વાકર્ષણ બળની વિરુદ્ધ $(3)$ થયેલું કાર્ય ઋણ $(c)$ કેન્દ્રગામી બળ વડે - 2$9 kg$ દળનો એક બોમ્બ $3 kg$ અને $6 kg$ દળના બે ટુકડાઓમાં વિસ્ફોટ પામે છે. $6 kg $ ના ટુકડાની ગતિ ઊર્જા $120 J$ તો $3 kg$ દળની ગતિ ઊર્જા ......... $J$ શોધો.View Solution
- 3$X- $ અક્ષની દિશામાં ગતિ કરવા માટે મુકત એવા $1\; kg $ દળના પદાર્થ માટે સ્થિતિ-ઊર્જા નીચેના સૂત્રથી મળે છે: $U\left( x \right) = \left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)$ $J $ તેની યાંત્રિક ઊર્જા $2\;J $ છે,તો તેની મહત્તમ ઝડપ $m/s$ માં કેટલી થાય?View Solution
- 4બે સમાન લાદીના ઢેફાઓને બાજુ બાજુએથી બે લાંબી દોરી વડે લટકાવેલા છે. એક બાજુ દોરવામાં આવે છે કે જેથી તેનું ગુરૂત્વકેન્દ્ર $h $ શિરોલંબ અંતર વધે છે. તેને મુક્ત કરવામાં આવે છે અને ત્યારે તે બીજા એક સાથે અસ્થિતિસ્થાપક રીતે સંઘાત પામે છે. તો આ સંયોજનના ગુરૂત્વકેન્દ્રથી વધેલા શિરોલંબ અંતર કેટલું હશે ?View Solution
- 5વેગમાન $P$ અને દળ $m$ ધરાવતી કાર રફ રોડ પર ગતિ કરે છે.જો ટાયર અને રોડ વચ્ચેનો ઘર્ષણાંક $m$ હોય,તો સ્ટોપિંગ ડીસ્ટન્સ કેટલું થશે?View Solution
- 6$10 \,kg$ દળનો એક પદાર્ચ $3 \,ms ^{-1}$ ઝડપથી ગતિ કરતો કરતો સ્થિર અવસ્થામાં રહેલાં $5 \,kg$ દળના બીજા પદાર્થ સાથે અથડામણા અનુભવે છે. પરિણામ સ્વરૂપે બંને એકબીજા સાથે ચોંટી જાય છે. સંયુક્ત દળની ગતિઊર્જા ............ $J$ હશે.View Solution
- 7એક માણસ સાઇકલ પર સવાર થઇને $7.2 km/hr$ વેગથી જેનો ઢાળ $20m $ અને ઊંચાઇ $1m$ હોય તેવા ઢોળાવ પર ગતિ કરે છે. માણસ અને સાઇકલનું કુલ દળ $100 kg$ છે. માણસનો પાવર કેટલા .....$W$ હશે?View Solution
- 8$100 m $ લંબાઇ અને $1 m$ ઉંચાઇ ધરાવતા ઢાળ પર $30,000 kg$ નો ટ્રક $30 km/hr$ ની ઝડપથી ગતિ કરે,તો ટ્રકનો પાવર કેટલા .......... $kW$ થશે? $( g = 10m{s^{ - 1}}) $View Solution
- 9જ્યારે પૃથ્વીની સપાટીથી અમુક ઉંચાઈ $P$ પરથી $0.4\,kg$ દળનું પતન કરવામાં આવે છે. ત્યારે તેને જમીન પર પહોંચવા માટે $8\,s$ લાગે છે. તો તેના પતનની અંતિમ સેકંડ દરમિયાન ગુમાવેલી સ્થિતિ ઊર્જા $...........J.$ $\left( g =10\,m / s ^2\right.$ લો)View Solution
- 10સ્થિર સ્થિતિમાં રહેલ $m$ દળના પદાર્થ પર અચળ બળ લાગવાના કારણે તે $d$ જેટલું અંતર કાપીને પ્રાપ્ત કરેલી ગતિઊર્જા $K$ કોના સમપ્રમાણમાં હશે?View Solution
