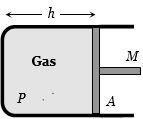
(a) Let the piston be displaced through distance \(x\) towards left, then volume decreases, pressure increases. If \(\Delta P\) is increase in pressure and \(\Delta V\) is decrease in volume, then considering the process to take place gradually (i.e. isothermal) \({P_1}{V_1} = {P_2}{V_2}\)
\( \Rightarrow PV = (P + \Delta P)(V - \Delta V)\)
\( \Rightarrow PV = PV + \Delta PV - P\Delta V - \Delta P\Delta V\)
\( \Rightarrow \Delta P.V - P.\Delta V = 0\) (neglecting \(\Delta P.\Delta V)\)
\(\Delta P(Ah) = P(Ax)\)
\( \Rightarrow \Delta P = \frac{{P.x}}{h}\)
This excess pressure is responsible for providing the restoring force \((F)\) to the piston of mass \(M\).
Hence \(F = \Delta P.A = \frac{{PAx}}{h}\)
Comparing it with \(|F| = kx\)
\(\Rightarrow k = M{\omega ^2} = \frac{{PA}}{h}\)
\( \Rightarrow \omega = \sqrt {\frac{{PA}}{{Mh}}} \)
\(\Rightarrow T = 2\pi \sqrt {\frac{{Mh}}{{PA}}} \)
Short trick : by checking the options dimensionally. Option (a) is correct.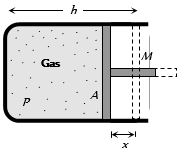
Download our appand get started for free
Similar Questions
- 1પ્રારંભિક કળા $ \pi /2 $ થી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $0.5\, cm$ અને આવર્તકાળ $0.4\, sec$ છે.તો તેની સરળ આવર્ત ગતિનું સમીકરણ નીચે પૈકી કયું થાય?View Solution
- 2$5\, gm$ દળ ધરાવતા પદાર્થનો કંપવિસ્તાર $10\,cm$ છે,તેનો મહત્તમ વેગ $100\,cm/sec$ છે.તો તેનો વેગ $50\, cm/sec$ કયાં અંતરે થાય?View Solution
- 3લીસી, સમક્ષિતિજ સપાટી પરના કોઇ પદાર્થના દોલનનું સમીકરણ $X= Acos\omega t$ છે,View Solution
જયાં $X=t$ સમયે સ્થાનાંતર
$\omega $ = દોલનની કોણીય આવૃત્તિ
નીચેનામાંથી કયો આલેખ $a$ નો $t$ સાથેનો ફેરફાર સાચી રીતે દર્શાવે છે?
અહી $a=t$ સમયે પ્રવેગ
$T=$ આવર્તકાળ
- 4View Solutionએક કણ નિયમિત ઝડપથી વર્તુળમાં ગતિ કરે છે. આ ગતિ .....
- 5એક કણ સરળ $a$ કંપવિસ્તાર અને $T$ આવર્તકાળથી સરળ આવર્તગતિ કરે છે. તો કણને $x = a$ થી $x = \frac{a }{2}$ જવા માટે કેટલો સમય લાગે?View Solution
- 6$x-$ અક્ષ પર મુક્ત રીતે ગતિ કરી શકતા કણની સ્થિતિ ઉર્જા $U(x) = k[1 - \exp {( - x)^2}]$ for $ - \infty \le x \le + \infty $ દ્વારા આપેલ છે. જ્યાં $k$ એ અનુરૂપ પરિમાણ માં ધન અચળાંક છે. તો.....View Solution
- 7$y = 2\, (cm)\, sin\,\left[ {\frac{{\pi t}}{2} + \phi } \right]$ સરળ આવર્તગતિમાં પ્રવેગનું મહત્તમ મૂલ્ય કેટલું થાય?View Solution
- 8$0.2 \mathrm{~kg}$ દળનો પદાર્થ $\left(\frac{25}{\pi}\right) \mathrm{Hz}$ આવૃત્તિ સાથે $\mathrm{x}$-અક્ષની દિશામા: સરળ આવર્ત ગતિ કરે છે. $x=0.04$ સ્થાને પદાર્થની ગતિ ઉર્જા $0.5 \mathrm{~J}$ અને સ્થિતિ ઉર્જા $0.4 \mathrm{~J}$ છે.દોલનનો કંપવિસ્તાર. . . . . . $\mathrm{cm}$.View Solution
- 9નીચેનામાંથી ક્યુ સૂત્ર સીધી રેખામાં સરળ આવર્ત ગતિ દર્શાવે છે. જ્યાં $x$ એ સ્થાનાંતર અને $a,b,c$ એ ઘન અચળાંક છે.View Solution
- 10સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $a$ અને આવર્તકાળ $T$ છે.સમતોલન બિંદુથી અડધા કંપવિસ્તાર સુધી પહોંચવા માટે કેટલો સમય લાગે?View Solution
