With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel. In the circuit diagram shown below, find:
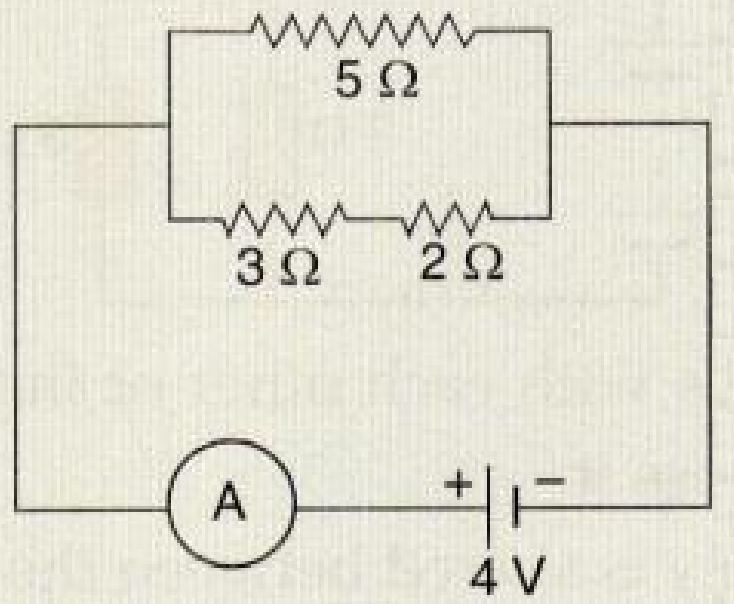
- Total resistance.
- Current shown by the ammeter $A$

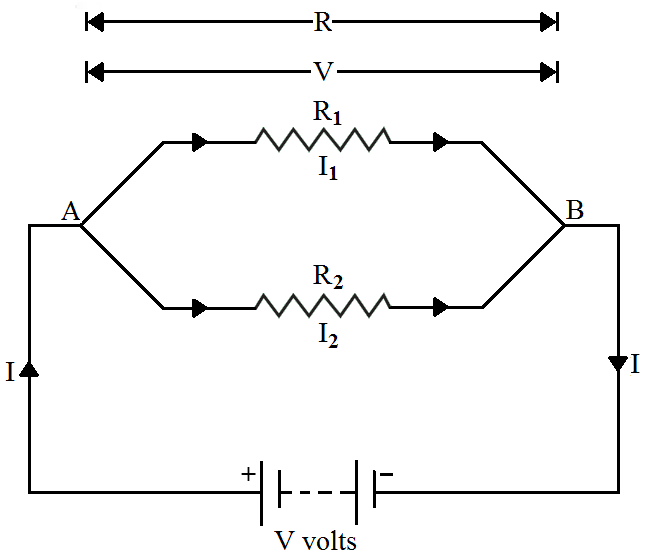
- Suppose total current flowing the circuit is I then the current passing through resistance $R_1 $ will be $I_1$ and current passing through resistance $R_2$ will be $I_2$
Let resultant resistance of this parallel combination is R. By applying the ohm's law to each resistance we get that,
$\text{I}_1=\frac{\text{V}}{\text{R}_1}$
$\text{I}_2=\frac{\text{V}}{\text{R}_2}$
putting these eq in the above one, we get that
$\frac{\text{V}}{\text{R}}=\frac{\text{V}}{\text{R}_1}+\frac{\text{V}}{\text{R}_2}$
$\frac{1}{\text{R}}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
If two resistance are connected in parallel than the resultant resistance will be
$\frac{1}{\text{R}}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
- Total resistance $= R$
$R_2 = 3 + 2 = 5$ ohms
$R_1 = 5$ ohm
$\frac{1}{\text{R}}=\frac{1}{5}+\frac{1}{5}$
$\frac{1}{\text{R}}=\frac{2}{5}$
$R = 2.5$ ohm
Current flows through the circuit
$\text{I}=\frac{\text{V}}{\text{R}}=\frac{4}{2.5}$
$= 1.6$ amps
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View SolutionHow does the resistance of a conductor depend on:
- Length of the conductor?
- Area of cross-section of the conductor?
- Temperature of the conductor?
- 2What possible values of resultant resistance one can get by combining two resistances, one of value $2$ ohm and the other $6$ ohm?View Solution
- 3In which of the following cases more electrical energy is consumed per hour?View Solution
- A current of $1$ ampere passed through a resistance of $300$ ohms.
- A current of $2$ amperes passed through a resistance of $100$ ohms.
- 4The resistors $R_1 , R_2 , R_3$ and $R_4$ in the figure given below are all equal in value.View Solution
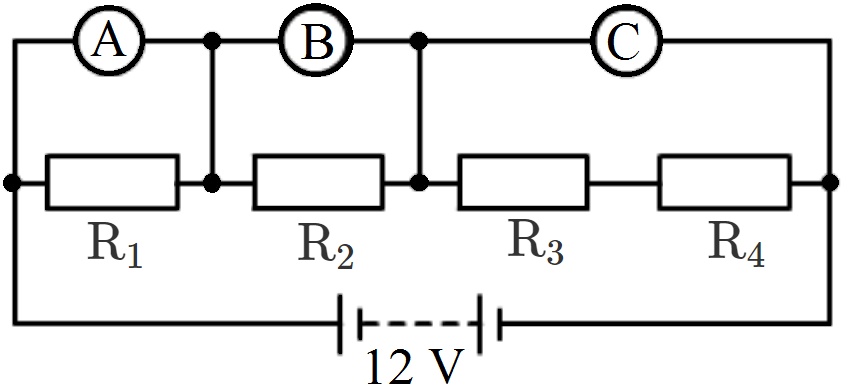
What would you expect the voltmeters $A, B$ and $C$ to read assuming that the connecting wires in the circuit have negligible resistance? - 5Calculate the resistance of a copper wire 1.0km long and 0.50mm diameter if the resistivity of copper is $1.7\times10\Omega\ \text{m}.$View Solution
- 6A wire is 1.0m long, 0.2mm in diameter and has a resistance of $10Ω.$ Calculate the resistivity of its material?View Solution
- 7Two resistances when connected in parallel give resultant value of $2$ ohm; when connected in series the value becomes $9$ ohm. Calculate the value of each resistance.View Solution
- 8How will you connect three resistors of resistances $2Ω, 3Ω$ and $6Ω $ obtain a total n si stance of:View Solution
- $4 Ω,$
- $1Ω$
- 9Calculate the area of cross-section of a wire if its length is 1.0m, its resistance is $23 Ω$ and the resistivity of the material of the wire is $1.84\times10 Ω\ \text{m}.$View Solution
- 10The electrical resistivities of three materials P, Q and R are given below:$\begin{matrix}\text{P}&2.3\times10^{3}\Omega\text{ m}\\\text{Q}&2.63\times10^{-8}\Omega\text{ m}\\\text{R}&1.0\times10^{15}\Omega\text{ m}\end{matrix}$View Solution
Which material will you use for making:- Electric wires.
- Handle for soldering iron, and
- Solar cells?
