Calculate the area of cross-section of a wire if its length is 1.0m, its resistance is $23 Ω$ and the resistivity of the material of the wire is $1.84\times10 Ω\ \text{m}.$
I = 1.0m
R = 23 ohm
$\rho=1.84\times10^{-6}\ \text{ohm-meter}$
We have
$\text{R}=\rho\frac{\text{I}}{\text{A}}$
$23=1.84\times10^{-6}\times\frac{1}{\text{A}}$
$\text{A}=\frac{1.84\times10^{-6}}{23}$
$=0.08\times10^{-6}\text{m}^2$
$=8\times10^{-8}\text{m}^2$
R = 23 ohm
$\rho=1.84\times10^{-6}\ \text{ohm-meter}$
We have
$\text{R}=\rho\frac{\text{I}}{\text{A}}$
$23=1.84\times10^{-6}\times\frac{1}{\text{A}}$
$\text{A}=\frac{1.84\times10^{-6}}{23}$
$=0.08\times10^{-6}\text{m}^2$
$=8\times10^{-8}\text{m}^2$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1What possible values of resultant resistance one can get by combining two resistances, one of value $2$ ohm and the other $6$ ohm?View Solution
- 2View SolutionConsider the circuit given below where A, B and C are three identical light bulbs of constant resistance.
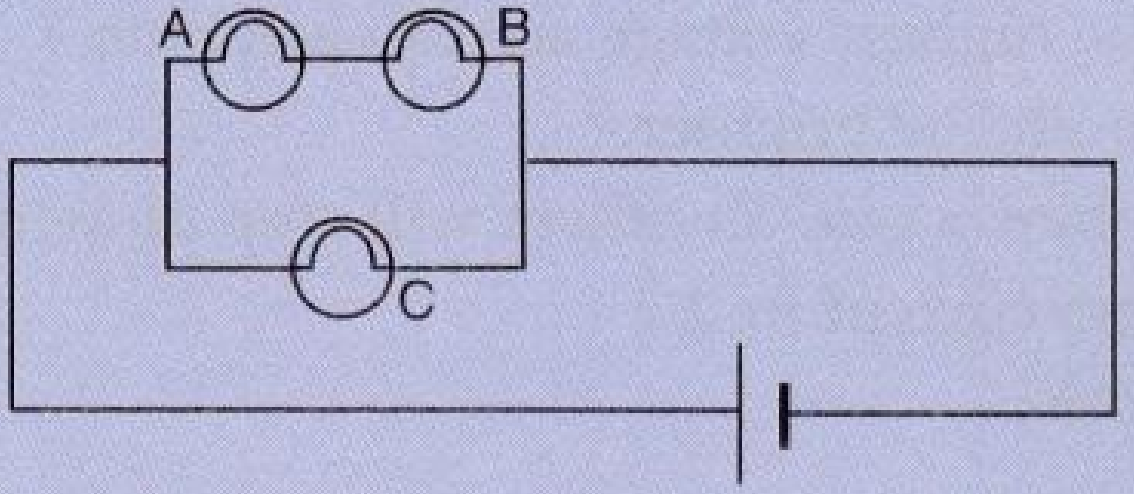
- List the bulbs in order of increasing brightness.
- If C burns out, what will be the brightness of A now compared with before?
- If B burns out instead, what will be the brightness of A and C compared with before?
- 3The resistors $R_1 , R_2 , R_3$ and $R_4$ in the figure given below are all equal in value.View Solution
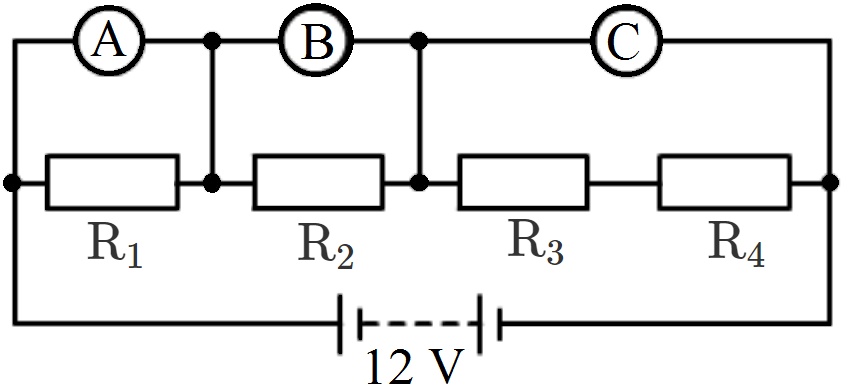
What would you expect the voltmeters $A, B$ and $C$ to read assuming that the connecting wires in the circuit have negligible resistance? - 4What will be the resistance of a metal wire of length $2$ metres and area of cross-section $1.55 \times 10m $, if the resistivity of the metal be $2.8 \times 10 m?$View Solution
- 5A $4 Ω$ coil and a $2 Ω$ coil are connected in parallel. What is their combined resistance? A total current of 3A passes through the coils. What current passes through the $2 Ω$ coil?View Solution
- 6For the circuit shown in the diagram below:View Solution
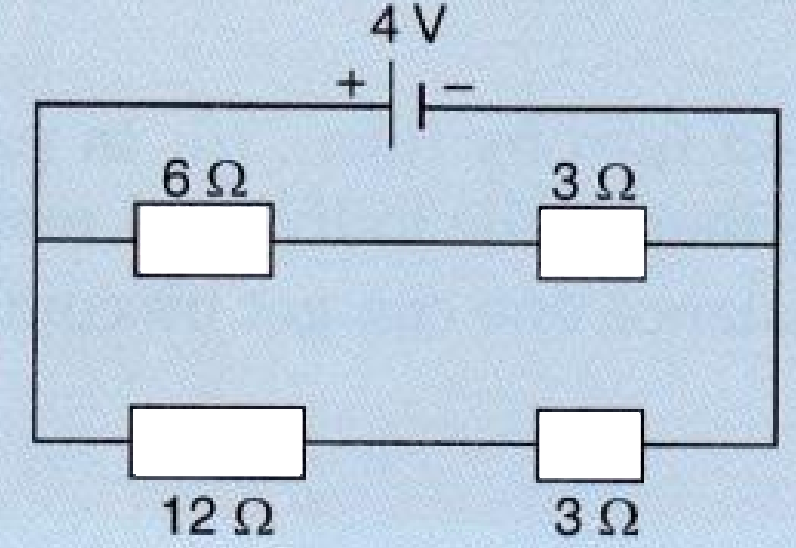
What is the value of :
Current through $6 Ω$ resistor?
Potential difference across $12 Ω$ resistor? - 7A flash of lightning carries $10\ C$ of charge which flows for $0.01\ s$. What is the current? If the voltage is $10MV$, what is the energy?View Solution
- 8View SolutionWhat is an ammeter? How is it connected in a circuit? Draw a diagram to illustrate your answer.
- 9View SolutionGive three reasons why different electrical appliances in a domestic circuit are connected in parallel.
- 10View SolutionA resistor has a resistance of 176 ohms. How many of these resistors should be connected in parallel so that their combination draws a current of 5 amperes from a 220 volt supply line?
