यदि F(x) = $ \left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right] $ है तो सिद्ध कीजिए कि F(x) F(y) = F(x + y)
Exercise-3.2-13
बायाँ पक्ष = F(x) F(y) =$ \left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]$$ \left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]$
= $\left[\begin{array}{ccc} \cos x \cos y-\sin x \sin y & -\sin y \cos x-\sin x \cos y & 0 \\ \sin x \cos y+\cos x \sin y & -\sin x \sin y+\cos x \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]$ [$ \because $ cos (A + B) = cos A cos B - sin A sin B, sin (A + B) = sin A cos B + sin B cos A]
= $\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]$
अब, F(x) में x को (x + y) के द्वारा प्रतिस्थापित करने पर,
$\therefore$ F(x + y) = $\left[\begin{array}{ccc}\sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1\end{array}\right]$
F(x) F(y) = F(x + y) = दायाँ पक्ष
= $\left[\begin{array}{ccc} \cos x \cos y-\sin x \sin y & -\sin y \cos x-\sin x \cos y & 0 \\ \sin x \cos y+\cos x \sin y & -\sin x \sin y+\cos x \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]$ [$ \because $ cos (A + B) = cos A cos B - sin A sin B, sin (A + B) = sin A cos B + sin B cos A]
= $\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]$
अब, F(x) में x को (x + y) के द्वारा प्रतिस्थापित करने पर,
$\therefore$ F(x + y) = $\left[\begin{array}{ccc}\sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1\end{array}\right]$
F(x) F(y) = F(x + y) = दायाँ पक्ष
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1परिकलित कीजिए: $\left[\begin{array}{cc} \cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x \end{array}\right]$ + $\left[\begin{array}{cc} \sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x \end{array}\right]$View Solution
- 2तीन फैक्ट्रियों I, II तथा III में पुरुष तथा महिला कर्मियों से संबंधित निम्नलिखित सूचना पर विचार कीजिए:View Solution
पुरुष कर्मी महिला कर्मी I 30 25 II 25 31 III 27 2 उपर्युक्त सूचना को एक 3 $ \times$ 2 आव्यूह में निरूपित कीजिए। तीसरी पक्ति और दूसरे स्तंभ वाली प्रविष्टि क्या प्रकट करती है?
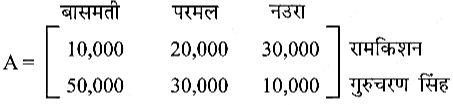
- 3View Solutionदो किसान रामकिशन और गुरचरन सिंह केवल तीन प्रकार के चावल जैसे बासमती, परमल तथा नउरा की खेती करते हैं। दोनों किसानों द्वारा, सितंबर तथा अक्तूबर माह में, इस प्रकार के चावल की बिक्री (रुपयों में) को, निम्नलिखित A तथा B आव्यूहों में व्यक्त किया गया है:
सितंबर माह की बिक्री (₹ में)
अक्तूबर माह की बिक्री (₹ में)
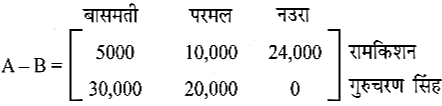
- प्रत्येक किसान की प्रत्येक प्रकार के चावल की सितंबर तथा अक्तूबर की सम्मिलित बिक्री ज्ञात कीजिए।
- सितंबर की अपेक्षा अक्तूबर में हुई बिक्री में कमी ज्ञात कीजिए।
- यदि दोनों किसानों को कुल बिक्री पर 2% लाभ मिलता है, तो अक्तूबर में प्रत्येक प्रकार के चावल की बिक्री पर प्रत्येक किसान को मिलने वाला लाभ ज्ञात कीजिए।
- 4X तथा Y ज्ञात कीजिए यदि X + Y = $ \left[\begin{array}{ll}7 & 0 \\ 2 & 5\end{array}\right]$ तथा X - Y = $\left[\begin{array}{ll}3 & 0 \\ 0 & 3\end{array}\right]$View Solution
- 5प्रदत्त समीकरण को x, y, z तथा t के लिए हल कीजिए यदिView Solution
2$\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]$+ 3$\left[\begin{array}{rr} 1 & -1 \\ 0 & 2 \end{array}\right]$ = 3$\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right] $ - 6आव्यूह का परिवर्त ज्ञात कीजिए: $\left[\begin{array}{c} 5 \\ \frac{1}{2} \\ -1 \end{array}\right]$View Solution
- 7परिकलित कीजिए: $\left[\begin{array}{rrr} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{array}\right]$ + $\left[\begin{array}{ccc} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{array}\right]$View Solution
- 8यदि $A = \left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]$ तथा $I = \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]$ एवं $A^2 = kA - 2I$ हो तो $k$ ज्ञात कीजिए।View Solution
- 9सिद्ध कीजिए कि आव्यूह A = $\left[\begin{array}{rrr} 0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0 \end{array}\right]$ एक विषम सममित आव्यूह है।View Solution
- 10A = $[a_{ij}]_{m \times n}$ एक वर्ग आव्यूह है यदिView Solution
