યંગના બે સ્લિટના પ્રયોગમાં શલાકાની પહોળાઈ $0.2 \,mm$ છે. જો પ્રકાશની તરંગલંબાઈ એ $10\%$ જેટલી વધે છે અને સ્લીટનું અંતર $10\%$ જેટલું વધે છે. તો શલાકાની પહોળાઈ .....$mm$
Medium
a
Given \(\beta_1=0.2\,mm\)
Given \(\beta_1=0.2\,mm\)
Let wavelength corresponding to \(\beta\), is \(\lambda\) and \(d\) be distance b/w slits. We know, \(\beta=\frac{\lambda D}{d}\)
for \(\beta_1=0.2 mm =\frac{\lambda D}{\lambda}-\) (1)
Now, \(\lambda\) and \(d\) are invereased by \(10 \%\) i.e
\(\lambda^{\prime}=\frac{11}{10} \lambda \text { and } d^{\prime}=\frac{11}{10} d.\)
\(\therefore \quad \beta_2=\frac{\lambda^{\prime} D}{d^{\prime}}=\frac{11}{10} \lambda \times D \times \frac{10}{11 d}=\frac{\lambda D}{d}-2\)
from \((1)\) and \((2)\)
\(\beta_2=0.2\,mm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પરસ્પર લંબ સમતલમાં તલધ્રુવીભૂત કિરણપૂંજ $A$ અને $B$ ને પોલેરોઇડ વડે જોડવામાં આવે છે.જયારે કિરણપુંજ $A$ મહત્તમ તીવ્રતા ( અને કિરણપુંજ $B$ શૂન્ય તીવ્રતા ) ધરાવતું હોય,તે સ્થિતિમાંથી પોલેરોઇડને $30°$ ના કોણે ભ્રમણ કરાવતા બંને કિરણપુંજો સમાન તીવ્રતાથી દેખાય છે.જો બંને કિરણપુંજોની પ્રારંભિક તીવ્રતા અનુક્રમે $I_A$ અને $I_B$ હોય,તો $\frac{{{I_A}}}{{{I_B}}}$=View Solution
- 2યંગના પ્રયોગમાં બે ઉદ્ગમ વચ્ચેનું અંતર $d=2\lambda$ હોય તો કેટલી મહતમ પ્રકાશિત શલાકા મળે?View Solution
- 3યંગના ડબલ સ્લિટના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $0.2\; mm $ અને સ્લિટ, પડદા વચ્ચેનું અંતર $200\; cm$ અને વપરાયેલ પ્રકાશની તરંગલંબાઈ $\lambda = 5000 \;\mathring A$ છે. મધ્યસ્થ અધિકતમ $x=0 $ પર છે. ત્રીજુ મહત્તમ (મધ્યસ્થ અધિકતમને શૂન્ય મહત્તમ લો) $x=.....cm$ અંતરે હોય?View Solution
- 4યંગના પ્રયોગમાં મઘ્યસ્થ અઘિકતમ અને $ 10 $ મી પ્રકાીશત શલાકાના $y-$ યામ $2 cm$ અને $5 cm $ છે.જો પ્રયોગ $1.5 $ વક્રીભવનાંક ઘરાવતા પ્રવાહીમાં કરવામાં આવે તો નવા યામ કેટલા થાય?View Solution
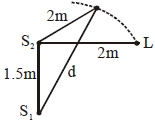
- 5બે સુસંબંધ ધ્વનિ ઉદગમાં $s_1$ અને $S_2$ એ $1\,m$ તરંગલંબાઈ ધરાવતા સમાન કળાના તરંગો ઉત્પન્ન કરે છે $S_{1}$ અને $S_{2}$ ને $1.5\,cm$ અંતરે રાખેલા છે. $S_{2}$ ની સામે $2\,m$ અંતરે રહેલા અવલોકનકાર $L$ ને લઘુતમ તીવ્ર્તાનો અવાજ સંભળાઈ છે જ્યારે અવલોકનકાર $S_1$ થી દૂર તરફ પરંતુ $S_2$ થી સમાન અંતરે રહીને ગતિ કરે ત્યારે તે જ્યારે $S_1$ થી $d$ અંતરે હોય ત્યારે મહતમ તીવ્ર્તા સંભળાઈ છે તો $d=......m$View Solution
- 6યંગના ડબલ સ્લીટના પ્રયોગમાં બે સ્લીટમાંથી એકની પહોળાઈ બીજી સ્લિટ કરતાં ત્રણ ગણી છે. જો સ્લીટમાંથી આવતા પ્રકાશનો કંપવિસ્તાર સ્લિટની પહોળાઈના સમપ્રમાણમાં હોય, વ્યતિકરણની ભાતમાં લઘુત્તમ અને મહત્તમ તીવ્રતાનો ગુણોત્તર $x: 4$ છે જ્યાં $x$ કેટલો હશે?View Solution
- 7$6 \times 10^{-7} \,m$ તરંગલંબાઈ ધરાવતું સમતલ તરંગ-અગ્ર $0.4 \,mm$ પહોળાઈની સ્લિટ પર આપાત કરવામાં આવે છે. સ્લિટની પાછળ $0.8 \,m$ કેન્દ્રલંબાઈનો બહિર્ગોળ લેન્સ મૂકતાં પડદા પર વિવર્તનભાત રચાય છે, તો બીજા અધિકતમની રેખીય પહોળાઈ કેટલા ............$mm$ હશે ?View Solution
- 8યંગના ડબલ સ્લિટનાં પ્રયોગમાં, શલાકાની પહોળાઈ $12\,mm$ છે.જો આખીય રચનાને $\frac{4}{3}$ જેટલો વક્રીભવનાંક ધરાવતા પાણીમાં ડૂબાડવામાં આવે તો શલાકાની પહોળાઈ $(mm$ માં) $..........$ થશે.View Solution
- 9યંગના ડબલ સ્લીટના પ્રયોગમાં બે સ્લીટ વચ્ચેનું અંતર સ્લીટની જાડાઈ કરતાં $6.1$ ગણું છે. તો એક સ્લીટ દ્વારા થતાં વિવર્તનમાં મધ્યસ્થ અધિકતમની અંદર મહત્તમ તીવ્રતા કેટલી વખત દેખાશે?View Solution
- 10$0.30 \,mm$ પહોળાઈની સ્લિટ પર $580\, nm$ તરંગલંબાઈનો એકવર્ણીય પ્રકાશ આપાત થાય છે. સ્લિટથી પડદા વચ્ચેનુ અંતર $2\, m$ છે. કેન્દ્રિય મહતમની પહોળાઈ ........... $\times 10^{-3} \,m$છે ?View Solution
