गैसों में ध्वनि का वेग किस बात पर निर्भर करता है?
[1988]
Download our app for free and get started
(b) किसी गैस में ध्वनि का वेग गैस के घनत्व तथा प्रत्यास्थता पर निर्भर करता है। अतः तीव्रता $\frac{2^2}{4^2}=\frac{1}{4}$ th
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
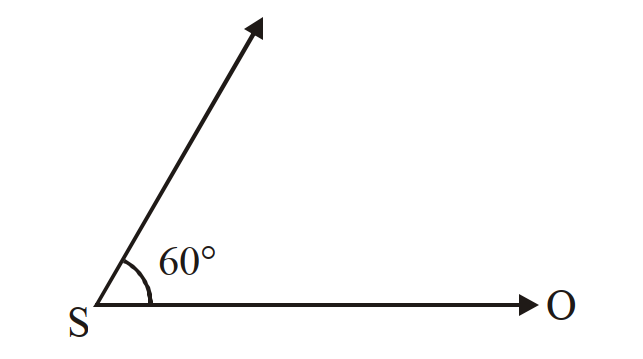
- 1$100 Hz$ आवृत्ति की ध्वनि उत्पन्न करता हुआ एक ध्वनि स्त्रोत $S$ तथा एक प्रेक्षक $O$, एक दूसरे से कुछ दूरी पर स्थित हैं। यह ध्वनि स्त्रोत, $19.4 \ ms ^{-1}$ की चाल से चल रहा है। उसके चलने की दिशा, स्त्रोत तथा प्रेक्षक की रिथितियों को मिलाने वाली सरलरेखा से $60^{\circ}$ का कोण बनाती है $($आरेख देखिये$)$। यदि, प्रेक्षक अपनी रिथति पर ही रूका रहता है तो, प्रेक्षक द्वारा सुनी गई ध्वनि की आभासी आवृत्ति होगी (हवा में ध्वनि का वेग $\left.330 \ ms ^{-1}\right)$ :View Solution
- 2View Solutionजब किसी माध्यम में अनुप्रस्थ तरंग चलती है तो कौन-सी विशेषता तरंग की चलने की दिशा में होगी
- 3एक आगामी तरंग $y =60 \cos (180 t -6 x )$ से प्रदर्शित होती है। जहां $y$ माइक्रॉन $t$ सेकंड व $x$ मीटर में है। अधिकतम कण वेग तथा तरंग वेग का अनुपात होगा$-$View Solution
- 4एक तारे में से $5000 \mathring A $ की तरंगे आती है जो पृथ्वी पर $1.50 \times 10^6$ मी/सेकंड से पहुंचती है। पृथ्वी पर पहुंचते हुए इसकी तरंग दैर्ध्य में क्या अंतर होगा?View Solution
- 5एक बंद आर्गन पाइप $P _1$ का पहला अधिस्वरक तथा खुले आर्गन पाइप $P _2$ का तीसरा अधिस्वरक अनुनाद में है। $P _1$ तथा $P _2$ की लम्बाईयों का अनुपात होगाView Solution
- 6दो कम्पित स्वरित्र प्रगामी तरंगें उत्पन्न करते हैं जो क्रमशः हैं $y _1=4 \sin 500 \pi t$ और $y _2=2 \sin 506 \pi t$. प्रति मिनट उत्पन्न विस्पंदों की संख्या है:View Solution
- 7$I _1$ और $I _2$ तीव्रताओं की दो आवर्ती तरंगें एक स्थानसे एक ही समय एक ही दिशा में गुजरती हैं। अधिकतम और न्यूनतम तीव्रताओं का जोड़ होगा :View Solution
- 8किस ताप पर ध्वनि का वेग इसके $27^{\circ} C$ ताप पर वेग का दोगुना होगाView Solution
- 9एक स्थायी तरंग $y = a \sin (100 t ) \cos (0.01 x )$ से प्रदर्शित की जाती है। जहां $y$ तथा $A$ मिमी में, $t$ सेकंड में तथा $x$ में है तो तरंग का वेग होगा-View Solution
- 10एक दूसरे के निकट स्थित ध्वनि के दो स्त्रोंतों निम्न प्रकार निरूपित प्रगामी तरंगें उत्सर्जित कर रहे है : $y_1=4 \sin 600 \pi t$ तथा $y_2=5 \sin 608 \pi t$. इन दोनों स्त्रोतों के निकट स्थित एक श्रोता को सुनाई देगा :View Solution