જો પ્રથમ ક્રમની $75 \%$ પ્રક્રિયા $90$ મિનિટમાં પૂર્ણ કરવામાં થઈ હતી, તો $60 \%$ સમાન પ્રક્રિયા પૂર્ણ થવા માટે લગભગ ........... સમય (મિનિટમાં) લાગશે
(લો: $\log 2=0.30 ; \log 2.5=0.40)$
JEE MAIN 2020, Medium
Download our app for free and get started
d
\(t _{0.75}=2 \times \frac{\ln 2}{ k }=90\)
\(t _{0.75}=2 \times \frac{\ln 2}{ k }=90\)
\(k =\frac{\ln 2}{45} min ^{-1}\)
\(kt =\ln \frac{1}{1-0.6}=\ln 2.5\)
\(\frac{\ln 2}{45} \times t=\ln 2.5\)
\(t=45 \times \frac{\log 2.5}{\log 2}=45 \times \frac{0.4}{0.3}=60 min\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રક્રિયા માટે થ્રેશોલ્ડ ઊર્જા કરતા વધારે ઉર્જાવાળા પરમાણુઓની સંખ્યા $27^{\circ}\, C$ થી $42^{\circ}\, C $ તાપમાનના વધારાથી પાંચ ગણો વધી જાય છે. તેની સક્રિયકરણની ઊર્જા.............. $J / mol$ છેView Solution
(લો : $\ln 5=1.6094;\left.R =8.314\, J mol ^{-1} K ^{-1}\right)$
- 2રાસાયણિક પ્રક્રિયામાં દાખલ થવા અણુઓ માટે ન્યુનતમ ઊર્જાને $.......$ કહે છે.View Solution
- 3એસિડ દ્રાવણમાં થતા એસિટોનના બ્રોમીનેશનને નીચેના સમીકરણ વડે દર્શાવાય છે.View Solution
$CH_3COCH_{3(aq)} + Br_{2(aq)} \rightarrow $$CH_3COCH_2Br_{(aq)} + H^+_{(aq)}+ Br^-_{(aq)}$
નીચેની પ્રક્રિયા સાંદ્રતા પરથી આ ગતિકીય માહિતી મળે છે.
શરૂઆતની સાંદ્રતા, $M$
$[CH_3COCH_3]$ $[Br_2]$ $[H^+]$ $0.30$ $0.05$ $0.05$ $0.30$ $0.10$ $0.05$ $0.30$ $0.10$ $0.10$ $0.40$ $0.05$ $0.20$ $Br_2$ ના દૂર થવાનો શરૂઆતનો દર $Ms^{-1}$ માં નીચે મુજબ છે.
$5.7 \times 10^{-5} ,$ $5.7 \times 10^{-5} ,$ $1.2 \times 10^{-5} ,$ $3.1 \times 10^{-5}$
આ માહિતીને આધારે વેગ સમીકરણ ...... થશે.
- 4પ્રક્રિયા $2 \mathrm{H}_{2}(\mathrm{g})+2 \mathrm{NO}(\mathrm{g}) \rightarrow \mathrm{N}_{2}(\mathrm{g})+2 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$ માટે અવલોકન વેગ રજૂઆત, વેગ $=\mathrm{k}_{\mathrm{f}}[\mathrm{NO}]^{2}\left[\mathrm{H}_{2}\right]$ છે. તો પ્રતિગામી પ્રક્રિયા માટે વેગ રજૂઆત જણાવો.View Solution
- 5જો $ t_{1/2} 20$ મિનિટ હોય તો $10 $ મિનિટ પછી પ્રથમ ક્રમની પ્રક્રિયકનો આંશિક ભાગ કેટલો?View Solution
- 6ફોર્મિક એસિડનું વિઘટન પર સોનાની સપાટી પ્રથમ ક્રમની ગતિને અનુસરે છે. જો $300\, K$ પર વેગ અચળાંક $1.0 \times 10^{-3} s ^{-1}$ છે અને સક્રિયકરણ ઊર્જા $E _{ a }=11.488\, kJ\, mol ^{-1}$ છે,$200\, K$ પર દર અચળાંક ............ $\quad \times 10^{-5} s ^{-1} .$View Solution
(આપેલ છે: $\left. R =8.314\, J\, mol ^{-1} K ^{-1}\right)$
- 7$700\, {~K}$ પર ${CaCO}_{3}$ના વિયોજન માટે પ્રથમ ક્રમનો દર અચળાંક $6.36 \times 10^{-3}\, {~s}^{-1}$ અને સક્રિયકરણ ઊર્જા $209\, {~kJ} \,{~mol}^{-1}$ છે. તેનો $500\, {~K}$ પર દર અચળાંક (${s}^{-1}$ માં) ${x} \times 10^{-6}$ છે. ${x}$નું મૂલ્ય $.....$ છે.(નજીકના પૂર્ણાંકમાં)View Solution
$[$આપેલ છે :${R}=8.31\, {~J} \,{~K}^{-1} \,{~mol}^{-1} ; \log 6.36 \times 10^{-3}=-2.19$ $\left.10^{-4.79}=1.62 \times 10^{-5}\right]$
- 8એઝોમિથેનના વિધટન માટે,View Solution
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
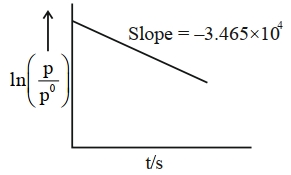
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]
- 9રેડીયો સમસ્થાનીક ટ્રીટીયમ $(_1^3H)$ નો અદ્ય આયુ સમય $12.3$ વર્ષ છે. જો ટ્રીટીયમનું પ્રારંભિક મુલ્ય $32\,mg,$ હોય તો $49.2$ વર્ષ પછી કેટલા મીલીગ્રામ બાકી રહેશે ?View Solution
- 10અર્ધ આયુષ્યના કિરણોત્સર્ગી નમૂના માટે ત્વરિત સમયે કિરણોત્સર્ગી વિઘટનનો દર$2.2 \times 10^{9}\; \mathrm{s}$$10^{10} \;\mathrm{s}^{-1}$છે .તે ઇન્સ્ટન્ટમાં તે નમૂનામાં કિરણોત્સર્ગી અણુઓની સંખ્યા કેટલી છે ?View Solution