Two exactly similar electric lamps are arranged (i) in parallel, and (ii) in series. If the parallel and series combination of lamps are connected to 220V supply line one by one, what will be the ratio of electric power consumed by them?
Let resistance of each lamp = R ohms.
Case1: Parellel connection
Resultant resistance $=\frac{1}{\frac{1}{\text{R}}+\frac{1}{\text{R}}}=\frac{\text{R}}{2}$
Electric power consumed $\text{P}_1=\frac{\text{V}_2}{\text{R}}=\frac{220^2}{\frac{\text{R}}{2}}=\frac{96800}{\text{R}}$
Case2: Series connection
Resultant resistance = R + R = 2R
Electric Power consumed $\text{P}_2=\frac{\text{V}^2}{2\text{R}}=\frac{24200}{\text{R}}$
$\therefore\frac{\text{P}_1}{\text{P}_2}=\frac{\frac{96800}{\text{R}}}{\frac{24200}{\text{R}}}=\frac{4}{1}$
Case1: Parellel connection
Resultant resistance $=\frac{1}{\frac{1}{\text{R}}+\frac{1}{\text{R}}}=\frac{\text{R}}{2}$
Electric power consumed $\text{P}_1=\frac{\text{V}_2}{\text{R}}=\frac{220^2}{\frac{\text{R}}{2}}=\frac{96800}{\text{R}}$
Case2: Series connection
Resultant resistance = R + R = 2R
Electric Power consumed $\text{P}_2=\frac{\text{V}^2}{2\text{R}}=\frac{24200}{\text{R}}$
$\therefore\frac{\text{P}_1}{\text{P}_2}=\frac{\frac{96800}{\text{R}}}{\frac{24200}{\text{R}}}=\frac{4}{1}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View SolutionWhat would be the effect on the resistance of a metal wire of:
- Increasing its length?
- Increasing its diameter?
- Increasing its temperature?
- 2View SolutionCalculate the cost of operating a heater of 500W for 20hours at the rate of? ₹3.90 per unit.
- 3View SolutionWhat is the resistance between A and B in the figure given below?
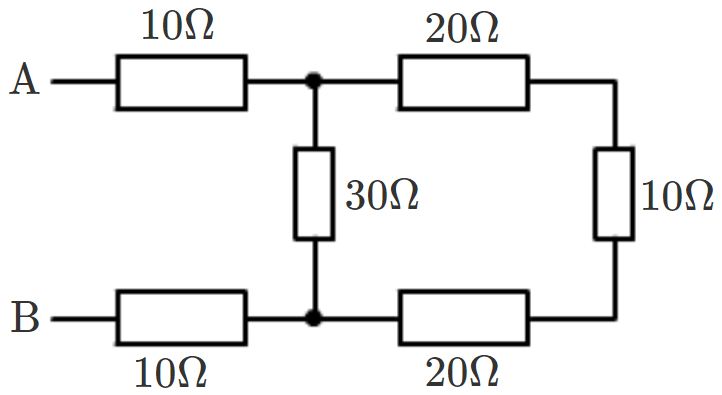
- 4View SolutionAn electric bulb is rated as 10W, 220V. How many of these bulbs can be connected in parallel across the two wires of 220V supply line if the maximum current which can be drawn is 5A?
- 5Calculate the resistance of a copper wire 1.0km long and 0.50mm diameter if the resistivity of copper is $1.7\times10\Omega\ \text{m}.$View Solution
- 6View SolutionWhat is a voltmeter? How is a voltmeter connected in the circuit to measure the potential difference between two points. Explain with the help of a diagram.
- 7You are given one hundred $1 \Omega $ resister. What is the smallest and largest resistance you can make in a circuit using these?View Solution
- 8View SolutionShow how you would connect two 4 ohm resistors to produce a combined resistance of:
- 2 ohms.
- 8 ohms.
- 9The electrical resistivities of five substances A, B, C, D and E are given below:View Solution
$\begin{matrix}\text{B}&110\times10^{-8}\Omega\text{ m}\\\text{C}&2.60\times10^{-8}\Omega\text{ m}\\\text{D}&10.0\times10^{-8}\Omega\text{ m}\\\text{E}&1.70\times10^{-8}\Omega\text{ m}\end{matrix}$ - 10The electrical resistivities of four materials $A, B, C$ and $D$ are given below:View Solution
$\text{A}\ -110\times10^{-8}\Omega\text{ m}$
$\text{B}-\ 1.0\times10^{10}\Omega\text{ m}$
$\text{C}-\ 10.0\times10^{-8}\Omega\text{ m}$
$\text{D}-\ 2.3\times10^{3}\Omega\text{ m}$
Which material is:- Good conductor.
- Resistor.
- Insulator, and
- Semiconductor
