Two resistances when connected in parallel give resultant value of $2$ ohm; when connected in series the value becomes $9$ ohm. Calculate the value of each resistance.
Two resistance when connected in series, resultant value is $9$ ohms.
Two resistance when connected in parallel, resultant values is $2$ ohms.
Let the two resistance be $R_1$ and $R_2$
If connected in series, then
$9 = R_1+ R_2$
$R_1 = 9 - R_2$
If connected in parallel, then
$\frac{1}{2}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
From aboves equations we get that
$\frac{1}{2}=\frac{(\text{R}_1+\text{R}_2)}{\text{R}_1\text{R}_2}$
$\frac{1}{2}=\frac{9}{(9-\text{R}_2)\text{R}_2}$
$9\text{R}_2-\text{R}_2{^2}=18$
$\text{R}_2{^2}-9\text{R}_2+18=0$
$(\text{R}_2-6)(\text{R}_2-3)=0$
$\text{R}_2=6,3$
So if $R_2= 6$ ohms, then $R_1 = 9 - 6 = 3 $ ohms.
If $R_2 = $3 ohms, then $R_1 = 9 - 3 = 6$ ohms.
Two resistance when connected in parallel, resultant values is $2$ ohms.
Let the two resistance be $R_1$ and $R_2$
If connected in series, then
$9 = R_1+ R_2$
$R_1 = 9 - R_2$
If connected in parallel, then
$\frac{1}{2}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
From aboves equations we get that
$\frac{1}{2}=\frac{(\text{R}_1+\text{R}_2)}{\text{R}_1\text{R}_2}$
$\frac{1}{2}=\frac{9}{(9-\text{R}_2)\text{R}_2}$
$9\text{R}_2-\text{R}_2{^2}=18$
$\text{R}_2{^2}-9\text{R}_2+18=0$
$(\text{R}_2-6)(\text{R}_2-3)=0$
$\text{R}_2=6,3$
So if $R_2= 6$ ohms, then $R_1 = 9 - 6 = 3 $ ohms.
If $R_2 = $3 ohms, then $R_1 = 9 - 3 = 6$ ohms.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1A piece of wire of resistance $20 Ω$ is drawn out so that its length is increased to twice its original length. Calculate the resistance of the wire in the new situation.View Solution
- 2View SolutionAn electric bulb is rated as 10W, 220V. How many of these bulbs can be connected in parallel across the two wires of 220V supply line if the maximum current which can be drawn is 5A?
- 3View SolutionShow how you would connect two 4 ohm resistors to produce a combined resistance of:
- 2 ohms.
- 8 ohms.
- 4View SolutionTen bulbs are connected in a series circuit to a power supply line. Ten identical bulbs are connected in a Parallel circuit to an identical power supply line.
- Which circuit would have the highest voltage across each bulb?
- In which circuit would the bulbs be brighter?
- In which circuit, if one bulb blows out, all others will stop glowing
- Which circuit would have less current in it?
- 5View SolutionWhat is Ohm’s law? Explain how it is used to define the unit of resistance.
- 6The resistors $R_1 , R_2 , R_3$ and $R_4$ in the figure given below are all equal in value.View Solution
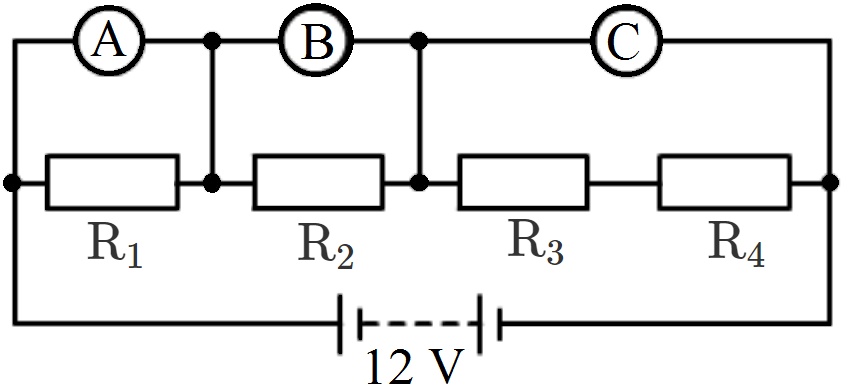
What would you expect the voltmeters $A, B$ and $C$ to read assuming that the connecting wires in the circuit have negligible resistance? - 7How will you connect three resistors of resistances $2Ω, 3Ω$ and $6Ω $ obtain a total n si stance of:View Solution
- $4 Ω,$
- $1Ω$
- 8Calculate the resistance of a copper wire 1.0km long and 0.50mm diameter if the resistivity of copper is $1.7\times10\Omega\ \text{m}.$View Solution
- 9In which of the following cases more electrical energy is consumed per hour?View Solution
- A current of $1$ ampere passed through a resistance of $300$ ohms.
- A current of $2$ amperes passed through a resistance of $100$ ohms.
- 10A wire is 1.0m long, 0.2mm in diameter and has a resistance of $10Ω.$ Calculate the resistivity of its material?View Solution
