1. x	0	2
   $y=\frac {x}{2}$	0	1

2. x	0	$\frac {20}{3}$	4
   y = $\frac {20 - 3x}{4}$	5	0	2

याद कीजिए कि प्रत्येक रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं। इसलिए आप कोई भी दो हल चुन सकते हैं, जो हमारे द्वारा चुने गए हलों से भी हो सकते हैं। क्या आप अनुमान लगा सकते हैं कि हमने पहले तथा दूसरे समीकरणों के हल के लिए, x = 0 क्यों चुना है? जब एक चर शून्य हो जाता है, तो समीकरण एक चर के रैखिक समीकरण में बदल जाता है, जिसे आसानी से हल किया जा सकता है। उदाहरण के लिए, समीकरण (2) में x = 0 रखने पर, हम पाते हैं कि 4y = 20 है, अर्थात् y = 5 है। इसी प्रकार, समीकरण (2) में y = 0 रखने पर हमें प्राप्त होता है:
3x = 20, अर्थात्, x = $\frac{20}{3}$ है। चूँक $\frac{20}{3}$ एक पूर्णांक नहीं है, इसलिए इसे ग्राफ पेपर पर ठीक-ठीक आलेखित करना आसान नहीं है। अतः हम y = 2 चुनते हैं, जिससे x = 4 मिलता है, जो एक पूर्णांक है।
सारणी के हलों के संगत बिंदुओं A(0, 0), B(2, 1) और P(0, 5), Q(4, 2) को आलेखित कीजिए। अब समीकरणों x - 2y = 0 और 3x + 4y = 20 को निरूपित करने वाली रेखाओं AB तथा PQ को खींचिए, जैसा कि आकृति में दर्शाया गया है।

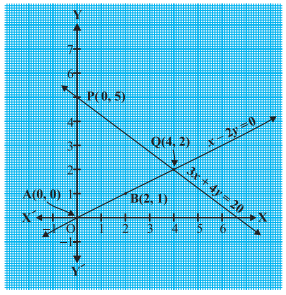
आकृति में ध्यान दीजिए कि दोनों समीकरणों को निरूपित करने वाली दोनों रेखाएँ बिंदु (4, 2) पर प्रतिच्छेद करती हैं। इसका क्या अर्थ है, इस पर हम अगले अनुच्छेद में चर्चा करेंगे।