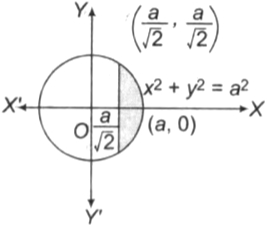
छेदक रेखा $x = \frac{a}{\sqrt{2}}$ द्वारा वृत्त $x^{2 }+ y^{2 }= a^2$ के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
Exercise-8.1-7
दिया है,
$x=\frac{a}{\sqrt{2}} ...(i)$
तथा वृत्त, $x^{2 }+ y^{2 }= a^2 ...(ii)$
चूँकि दी गई रेखा वृत्त को प्रतिच्छेदित करती है, अतः समी $(ii)$ में $x = \frac{a}{\sqrt{2}}$ रखने पर हमें प्राप्त होगा
$\left(\frac{a}{\sqrt{2}}\right)^{2}+y^{2}=a^{2}$
$\Rightarrow y^{2}=\frac{a^{2}}{1}-\frac{a^{2}}{2}=\frac{a^{2}}{2}$
$\Rightarrow |y|=\frac{a}{\sqrt{2}} \Rightarrow y$ $=\pm \frac{a}{\sqrt{2}}$
जब $y=\frac{a}{\sqrt{2}}$ $ \Rightarrow x^{2}=a^{2}-\left(\frac{a^{2}}{2}\right)$
$x^{2}=\frac{a^{2}}{2} $ $\Rightarrow x=\pm \frac{a}{\sqrt{2}}$
$\therefore$ प्रथम चतुर्थांश में $\left(\frac{a}{\sqrt{2}}, \frac{a}{\sqrt{2}}\right)$ प्रतिच्छेदक बिंदु हैं।
$\therefore$ अभीष्ट क्षेत्रफल $= 2 \times ($केवल प्रथम चतुर्थांश में छायांकित क्षेत्र का क्षेत्रफल$)$
$=2 \int_{a / \sqrt{2}}^{a}|y| d x=2 \int_{a / \sqrt{2}}^{a} \sqrt{a^{2}-x^{2}} d x$$=2\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]_{a / \sqrt{2}}^{a}$
$\left[\because \int \sqrt{a^{2}-x^{2}} d x\right.$$\left.=\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]$
$=2\left[0+\frac{a^{2}}{2} \sin ^{-1}(1)\right.$$\left.-\frac{a}{2 \sqrt{2}} \sqrt{a^{2}-\frac{a^{2}}{2}}-\frac{a^{2}}{2} \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]$
$=2\left[\frac{a^{2}}{2}\left(\frac{\pi}{2}\right)-\frac{a}{2 \sqrt{2}} \cdot \frac{a}{\sqrt{2}}-\frac{a^{2}}{2}\left(\frac{\pi}{4}\right)\right]$
$=2\left[\frac{a^{2} \pi}{4}-\frac{\pi a^{2}}{8}-\frac{a^{2}}{4}\right]$$=\left(\frac{a^{2} \pi}{4}-\frac{a^{2}}{2}\right)=\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$ वर्ग इकाई
अतः छेदक रेखा $x = \frac{a}{\sqrt{2}}$ द्वारा वृत्त $x^{2 }+ y^{2 }= a^2$^ के छोटे भाग का क्षेत्रफल $\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$ वर्ग इकाई है।
$x=\frac{a}{\sqrt{2}} ...(i)$
तथा वृत्त, $x^{2 }+ y^{2 }= a^2 ...(ii)$
चूँकि दी गई रेखा वृत्त को प्रतिच्छेदित करती है, अतः समी $(ii)$ में $x = \frac{a}{\sqrt{2}}$ रखने पर हमें प्राप्त होगा

$\left(\frac{a}{\sqrt{2}}\right)^{2}+y^{2}=a^{2}$
$\Rightarrow y^{2}=\frac{a^{2}}{1}-\frac{a^{2}}{2}=\frac{a^{2}}{2}$
$\Rightarrow |y|=\frac{a}{\sqrt{2}} \Rightarrow y$ $=\pm \frac{a}{\sqrt{2}}$
जब $y=\frac{a}{\sqrt{2}}$ $ \Rightarrow x^{2}=a^{2}-\left(\frac{a^{2}}{2}\right)$
$x^{2}=\frac{a^{2}}{2} $ $\Rightarrow x=\pm \frac{a}{\sqrt{2}}$
$\therefore$ प्रथम चतुर्थांश में $\left(\frac{a}{\sqrt{2}}, \frac{a}{\sqrt{2}}\right)$ प्रतिच्छेदक बिंदु हैं।
$\therefore$ अभीष्ट क्षेत्रफल $= 2 \times ($केवल प्रथम चतुर्थांश में छायांकित क्षेत्र का क्षेत्रफल$)$
$=2 \int_{a / \sqrt{2}}^{a}|y| d x=2 \int_{a / \sqrt{2}}^{a} \sqrt{a^{2}-x^{2}} d x$$=2\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]_{a / \sqrt{2}}^{a}$
$\left[\because \int \sqrt{a^{2}-x^{2}} d x\right.$$\left.=\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]$
$=2\left[0+\frac{a^{2}}{2} \sin ^{-1}(1)\right.$$\left.-\frac{a}{2 \sqrt{2}} \sqrt{a^{2}-\frac{a^{2}}{2}}-\frac{a^{2}}{2} \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]$
$=2\left[\frac{a^{2}}{2}\left(\frac{\pi}{2}\right)-\frac{a}{2 \sqrt{2}} \cdot \frac{a}{\sqrt{2}}-\frac{a^{2}}{2}\left(\frac{\pi}{4}\right)\right]$
$=2\left[\frac{a^{2} \pi}{4}-\frac{\pi a^{2}}{8}-\frac{a^{2}}{4}\right]$$=\left(\frac{a^{2} \pi}{4}-\frac{a^{2}}{2}\right)=\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$ वर्ग इकाई
अतः छेदक रेखा $x = \frac{a}{\sqrt{2}}$ द्वारा वृत्त $x^{2 }+ y^{2 }= a^2$^ के छोटे भाग का क्षेत्रफल $\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$ वर्ग इकाई है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1दीर्घवृत्त $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
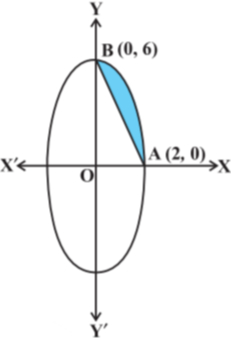
- 2आकृति में $\text{AOBA}$ प्रथम चतुर्थांश में दीर्घवृत्त $9x^{2 }+ y^{2 }= 36$ का एक भाग है जिसमें $OA = 2$ इकाई तथा $OB = 6$ इकाई है। लघु चाप $AB$ एवं जीवा $AB$ के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 3सिद्ध कीजिए कि वक्र $y^2 = 4x$ एवं $x^{2 }= 4y,$ रेखाओं $x = 0, x = 4, y = 4$ एवं $y = 0$ से घिरे वर्ग के क्षेत्रफल को तीन बराबर भागों में विभाजित करते हैं।View Solution
- 4दीर्घवृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ एवं रेखा $\frac{x}{a}+\frac{y}{b}=1$ से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 5परवलय $x^2 = y,$ रेखा $y = x + 2$ एवं $x-$अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 6वक्र $x^{2 }= 4y$ एवं रेखा $x = 4y - 2$ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 7समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के समीकरण $y = 2x + 1, y = 3x + 1$ एवं $x = 4$ हैं।View Solution
- 8प्रथम चतुर्थांश में $x^{2 }= 4y, y = 2, y = 4$ एवं $y-$अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 9समाकलन विधि का उपयोग करते हुए एक ऐसे त्रिभुज $\text{ABC}$, का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक $A(2, 0), B(4, 5)$ एवं $C(6, 3)$ हैं।View Solution
- 10यदि वक्र $x = y^2$ एवं रेखा $x = 4$ से घिरा हुआ क्षेत्रफल रेखा $x = a$ द्वारा दो बराबर भागों में विभाजित होता है तो $a$ का मान ज्ञात कीजिए।View Solution
