f के असांतत्य के बिंदुओं को ज्ञात करके, जब कि 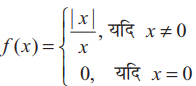 है।
है।
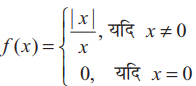 है।
है।Exercise-5.1-8
यहाँ, 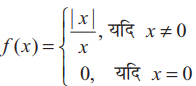
अब, LHL = $\lim \limits_{x \rightarrow 0^{-}} $ f(x) = $\lim \limits_{x \rightarrow 0^{-}}$ $ \frac{|x|}{x}$
x = 0 - h रखने पर, x $\rightarrow 0^{-}$ $\Rightarrow$ h $\rightarrow$ 0
$\Rightarrow$ $\lim \limits_{h \rightarrow 0}$ $\frac{|0-h|}{0-h}$ = $ \lim \limits_{h \rightarrow 0}$ $\frac{h}{-h}$ = - 1 $[\because|-h|$ = h$]$
तथा RHL = $\lim \limits_{x \rightarrow 0^{+}}$ f(x) = $\lim \limits_{x \rightarrow 0^{+}}$ $\frac{|x|}{x}$
x = 0 + h रखने पर $x \rightarrow 0^{+}$ $\Rightarrow$ h $\rightarrow$ 0 $ \Rightarrow $ $\lim \limits_{h \rightarrow 0}$ $\frac{|0+h|}{0+h}$ = $\lim \limits_{h \rightarrow 0} $ $\frac{h}{h}$ = 1
$\therefore$ LHL $ \neq $ RHL
अतः f(x), x = 0 पर असतत् फलन है।
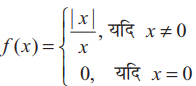
अब, LHL = $\lim \limits_{x \rightarrow 0^{-}} $ f(x) = $\lim \limits_{x \rightarrow 0^{-}}$ $ \frac{|x|}{x}$
x = 0 - h रखने पर, x $\rightarrow 0^{-}$ $\Rightarrow$ h $\rightarrow$ 0
$\Rightarrow$ $\lim \limits_{h \rightarrow 0}$ $\frac{|0-h|}{0-h}$ = $ \lim \limits_{h \rightarrow 0}$ $\frac{h}{-h}$ = - 1 $[\because|-h|$ = h$]$
तथा RHL = $\lim \limits_{x \rightarrow 0^{+}}$ f(x) = $\lim \limits_{x \rightarrow 0^{+}}$ $\frac{|x|}{x}$
x = 0 + h रखने पर $x \rightarrow 0^{+}$ $\Rightarrow$ h $\rightarrow$ 0 $ \Rightarrow $ $\lim \limits_{h \rightarrow 0}$ $\frac{|0+h|}{0+h}$ = $\lim \limits_{h \rightarrow 0} $ $\frac{h}{h}$ = 1
$\therefore$ LHL $ \neq $ RHL
अतः f(x), x = 0 पर असतत् फलन है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionf के असांतत्य के बिंदुओं को ज्ञात करके, जब कि
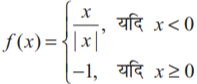 है।
है। - 2View Solutionf के असांतत्य के बिंदुओं को ज्ञात करके, जब कि
 है।
है। - 3$y = \sin^{-1} (2 x \sqrt{1-x^{2}}), - \frac{1}{\sqrt{2}} < x < \frac{1}{\sqrt{2}}$ में $\frac{d y}{d x}$ ज्ञात कीजिए।View Solution
- 4$f$ के असांतत्य के बिंदुओं को ज्ञात करके, जब किView Solution
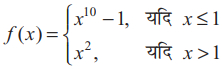 है।
है। - 5cos x $ \cdot$ cos 2x $ \cdot$ cos 3x प्रदत्त फलनों का x के सापेक्ष अवकलन कीजिए।View Solution
- 6$(\cos x)^{y }= (\cos y)^{x }$ में प्रदत्त फलनों के लिए $\frac{d y}{d x}$ ज्ञात कीजिए।View Solution
- 7$f$ के असांतत्य के बिंदुओं को ज्ञात करके, जब किView Solution
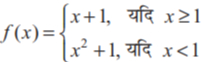 है।
है। - 8View Solutionफलन f, के सांतत्य पर विचार कीजिए, जहाँ f द्वारा परिभाषित है:

- 9View Solutionक्या
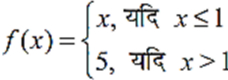 द्वारा परिभाषित फलन f
द्वारा परिभाषित फलन f
x = 0, x = 1, तथा x = 2 पर संतत है? - 10View Solutionf के असांतत्य के बिंदुओं को ज्ञात करके, जब कि
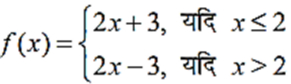 है।
है।
