दिए गए समीकरण हैं
$\frac { x } { 10 } + \frac { y } { 5 } - 1$ = 0 ... (i)
and $ \frac { x } { 8 } + \frac { y } { 6 }$ = 15 ... (ii) 
समीकरण (i) को 20 से और (ii) को 24 से गुणा करने पर हमें प्राप्त होता है
2x + 4y = 20 ... (iii)
3x + 4y = 360 ... (iv)

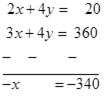
$\Rightarrow$ x = 340
अब, 2x + 4y = 20 ... [(iii) से]
2 से भाग देने पर हमें प्राप्त होता है
$\Rightarrow$ x + 2y = 10
x = 340 रखने पर हमें प्राप्त होता है
$\Rightarrow$ 340 + 2y = 10
$\Rightarrow$ 2y = 10 – 340
$\Rightarrow$ 2y = –330
$\Rightarrow y = \frac { - 330 } { 2 }$ = -165
अब, y = $\lambda$x + 5 ... [दिया गया है]
x = 340 और y = -165, y = $\lambda$x + 5 समीकरण में रखने पर हमें प्राप्त होता है
$\Rightarrow$ –165 = $\lambda$(340) + 5 
$\Rightarrow$ –$\lambda$(340) = 5 + 165
$\Rightarrow$ –$\lambda$(340) = 170
$\Rightarrow \quad \lambda = \frac { 170 } { - 340 } \Rightarrow \lambda = - \frac { 1 } { 2 }$
अत: दिए गए समीकरण युग्म का हल है x = 340, y = –165 और $ \lambda = - \frac { 1 } { 2 }$