समीकरणों के युग्म को हल कीजिए:
$\frac{x}{a}+\frac{y}{b} = a + b$
$\frac{x}{a^{2}}+\frac{y}{b^{2}} = 2, a, b \neq 0$
$\frac{x}{a}+\frac{y}{b} = a + b$
$\frac{x}{a^{2}}+\frac{y}{b^{2}} = 2, a, b \neq 0$
Exercise-3.3-9(6)
समीकरणों की दी गई प्रणाली को इस प्रकार लिखा जा सकता है:
$\frac{1}{a} \cdot x+\frac{1}{b} \cdot y-(a+b) = 0$
$\frac{1}{a^{2}} \cdot x+\frac{1}{b^{2}} \cdot y-2 = 0$
वज्र$-$गुणन से, हमारे पास है
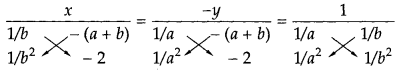
$\Rightarrow \frac { x } { \frac { 1 } { b } \times ( - 2 ) - \frac { 1 } { b ^ { 2 } } \times - ( a + b ) } = \frac { - y } { \frac { 1 } { a } \times - 2 - \frac { 1 } { a ^ { 2 } } \times - ( a + b ) } = \frac { 1 } { \frac { 1 } { a } \times \frac { 1 } { b ^ { 2 } } - \frac { 1 } { a ^ { 2 } } \times \frac { 1 } { b } }$
$ \Rightarrow \frac { x } { - \frac { 2 } { b } + \frac { a } { b ^ { 2 } } + \frac { 1 } { b } } = \frac { - y } { - \frac { 2 } { a } + \frac { 1 } { a } + \frac { b } { a ^ { 2 } } } = \frac { 1 } { \frac { 1 } { a b ^ { 2 } } - \frac { 1 } { a ^ { 2 } b } }$
$ \Rightarrow \frac { x } { \frac { a } { b ^ { 2 } } - \frac { 1 } { b } } = \frac { - y } { - \frac { 1 } { a } + \frac { b } { a ^ { 2 } } } = \frac { 1 } { \frac { 1 } { a b ^ { 2 } } - \frac { 1 } { a ^ { 2 } b } }$
$ \Rightarrow \frac { \frac { x } { a - b } } { \frac { a - b } { b ^ { 2 } } } = \frac { y } { \frac { a - b } { a ^ { 2 } } } = \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } }$
$ \Rightarrow x = \frac { a - b } { b ^ { 2 } } \times \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } } = a ^ { 2 }$ तथा $ y = \frac { a - b } { a ^ { 2 } } \times \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } } = b ^ { 2 }$
अत: $x = a^2, y = b^2$ दिए गए समीकरणों के निकाय का हल है।
$\frac{1}{a} \cdot x+\frac{1}{b} \cdot y-(a+b) = 0$
$\frac{1}{a^{2}} \cdot x+\frac{1}{b^{2}} \cdot y-2 = 0$
वज्र$-$गुणन से, हमारे पास है
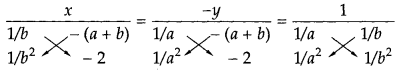
$\Rightarrow \frac { x } { \frac { 1 } { b } \times ( - 2 ) - \frac { 1 } { b ^ { 2 } } \times - ( a + b ) } = \frac { - y } { \frac { 1 } { a } \times - 2 - \frac { 1 } { a ^ { 2 } } \times - ( a + b ) } = \frac { 1 } { \frac { 1 } { a } \times \frac { 1 } { b ^ { 2 } } - \frac { 1 } { a ^ { 2 } } \times \frac { 1 } { b } }$
$ \Rightarrow \frac { x } { - \frac { 2 } { b } + \frac { a } { b ^ { 2 } } + \frac { 1 } { b } } = \frac { - y } { - \frac { 2 } { a } + \frac { 1 } { a } + \frac { b } { a ^ { 2 } } } = \frac { 1 } { \frac { 1 } { a b ^ { 2 } } - \frac { 1 } { a ^ { 2 } b } }$
$ \Rightarrow \frac { x } { \frac { a } { b ^ { 2 } } - \frac { 1 } { b } } = \frac { - y } { - \frac { 1 } { a } + \frac { b } { a ^ { 2 } } } = \frac { 1 } { \frac { 1 } { a b ^ { 2 } } - \frac { 1 } { a ^ { 2 } b } }$
$ \Rightarrow \frac { \frac { x } { a - b } } { \frac { a - b } { b ^ { 2 } } } = \frac { y } { \frac { a - b } { a ^ { 2 } } } = \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } }$
$ \Rightarrow x = \frac { a - b } { b ^ { 2 } } \times \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } } = a ^ { 2 }$ तथा $ y = \frac { a - b } { a ^ { 2 } } \times \frac { 1 } { \frac { a - b } { a ^ { 2 } b ^ { 2 } } } = b ^ { 2 }$
अत: $x = a^2, y = b^2$ दिए गए समीकरणों के निकाय का हल है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1समीकरणों के युग्म का हल कीजिए:View Solution
x + y = 3.3,
$\frac{0.6}{3 x-2 y}$ = -1, 3x - 2y $\neq$ 0 - 2View Solutionरेखाओं 5x - y = 5, x + 2y = 1 और 6x + y = 17 द्वारा बनने वाले त्रिभुज के शीर्ष बीजीय विधि से निर्धारित कीजिए।
- 3View Solutionदो वर्ष पहले, सलीम की आयु अपनी पुत्री की आयु की तिगुनी थी तथा छ: वर्ष बाद उसकी आयु पुत्री की आयु के दुगुने से चार वर्ष अधिक होगी। उनकी वर्तमान आयु क्या है?
- 4आलेखीय विधि से ज्ञात कीजिए कि $x – 2y = 6$ तथा $3x – 6y = 0$ समीकरण$-$युग्म संगत हैं या नहीं। यदि संगत हैं, तो इन्हें हल कीजिए।View Solution
- 5समीकरण$-$युग्म में $p$ का मान ज्ञात कीजिए: $-3x + 5y = 7$ और $2px – 3y = 1,$View Solution
यदि इन समीकरणों द्वारा निरूपित रेखाएँ एक अद्वितीय बिंदु पर प्रतिच्छेद करती हैं। - 6दो सीधे पथ समीकरणों $x - 3y = 2$ और $-2x + 6y = 5$ द्वारा निरूपित हैं। जाँच कीजिए कि ये पथ परस्पर काटते हैं या नहीं।View Solution
- 7समीकरण$-$युग्म में $p$ का मान ज्ञात कीजिए: $3x – y – 5 = 0$ और $6x – 2y – p = 0$View Solution
यदि इन समीकरणों द्वारा निरूपित रेखाएँ समांतर हैं। - 8View Solutionरेखाओं x = -2 और y = 3 के आलेख खींचिए। इन रेखाओं, x-अक्ष और y-अक्ष द्वारा बनी आकृति के शीर्ष लिखिए। इस आकृति का क्षेत्रफल भी ज्ञात कीजिए।
- 9View Solutionदो पाइपों द्वारा एक स्वीमिंग पूल को भरने में 12 घंटे लगते हैं। यदि इनमें से बड़े व्यास वाले पाइप का प्रयोग 4 घंटे करें और छोटे व्यास वाले पाइप का प्रयोग 9 घंटे करें, तो स्वीमिंग पूल केवल आधा ही भरा जा सकता है। प्रत्येक पाइप पृथक-पृथक रूप से स्वीमिंग पूल को कितने समय में भर पाएगा?
- 10समीकरण$-$युग्म में $p$ का मान ज्ञात कीजिए: $2x + 3y – 5 = 0$ और $px – 6y – 8 = 0,$View Solution
यदि समीकरण$-$युग्म का एक अद्वितीय हल है।
