दिए गए प्रश्न के अनुसार

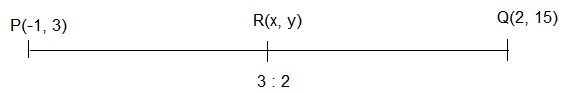
चूंकि PR = $\frac{3}{5}$
$\Rightarrow \frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{5}{3}$ 
$\Rightarrow \frac{\mathrm{PR}+\mathrm{PQ}}{\mathrm{PR}}=\frac{5}{3}$ 
$\Rightarrow 1+\frac{\mathrm{RQ}}{\mathrm{PR}}=\frac{5}{3}$ 
$\Rightarrow \frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{5}{3}-1=\frac{2}{3}$ 
$\therefore$ RQ : PR = 2 : 3
या PR : RQ = 3 : 2
मान लें कि R (x, y) वह बिंदु है जो बिंदु P (-1, 3) और Q (2, 5) को मिलाने वाले रेखाखंड को विभाजित करता है। अनुपात 3:2
$\therefore$ (x, y) = $\left\{\frac{3(2)+2(-1)}{3+2}, \frac{3(5)+2(3)}{3+2}\right\}$ 
$\because$ आंतरिक अनुभाग सूत्र द्वारा;
= $\left(\frac{m_{2} x_{1}+m_{1} x_{2}}{m_{1}+m_{2}}, \frac{m_{2} y_{1}+m_{1} y_{2}}{m_{1}+m_{2}}\right)$
= $\left(\frac{6-2}{5}, \frac{15+6}{5}\right)=\left(\frac{4}{5}, \frac{21}{5}\right)$ 
अत: बिंदु R के अभीष्ट निर्देशांक हैं $\left(\frac{4}{5}, \frac{21}{5}\right)$