दो अन्न भंडारों A और B की भंडारण क्षमता क्रमशः 100 क्विंटल और 50 क्विंटल है। उन्हें तीन राशन की दुकानों D, E और F पर अन्न उपलब्ध कराना पड़ता है, जिनकी आवश्यकताएँ क्रमशः 60, 50, और 40 क्विंटल हैं।
भंडारों से दुकानों को प्रति क्विंटल परिवहन व्यय निम्न सारणी के अनुसार है:
भंडारों से दुकानों को प्रति क्विंटल परिवहन व्यय निम्न सारणी के अनुसार है:
| प्रति क्विंटल परिवहन व्यय (रुपयों में) | ||
| को / से | A | B |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
परिवहन व्यय के न्यूनतमीकरण के लिए आपूर्ति का परिवहन कैसे किया जाए? न्यूनतम परिवहन मूल्य क्या है?
Miscellaneous Exercise-6
Download our app for free and get started
मान लीजिए भंडार A, दुकानों D तथा E को क्रमशः x क्विंटल तथा y क्विंटल अन्न उपलब्ध कराता हैं, तो दुकान F को (100 - x - y) क्विंटल अन्न उपलब्ध कराएगा दुकान D पर 60 क्विंटल अन्न की आवश्यकता है। चूँकि भंडार A से x क्विंटल अन्न उपलब्ध कराया जाता है। अतः शेष (60-x) क्विंटल अन्न भंडार B से उपलब्ध कराया जाता है। इसी प्रकार; (50 - y) क्विंटल अन्न तथा [40 - (100 - x - y)] =(x + y - 60) क्विंटल अन्न भंडार B से क्रमशः दुकानों E तथा F को उपलब्ध कराता है। दी गई समस्या को निम्न ग्राफ द्वारा निरूपित किया जा सकता है। मान लीजिए परिवहन की कुल लागत Z है।
अतः हमको उद्देश्य फलन
Z = 6x + 3y + 2.50(100 - x - y) + 4(60 - x) + 2(50 - y) + 3(x + y) - 60)
= 6x + 3y + 250 - 2.5x - 2.5y + 240 - 4x + 100 - 2y + 3x + 3y - 180
= 2.50x + 1.50y + 410 ...(i)
का निम्नतम मान निम्न व्यवरोधों के अंतर्गत ज्ञात करना है।
60 - x $\geq$ 0 $\Leftrightarrow$ x $\leq$ 60 ...(ii)
50 - y $\geq$ 0 $\Leftrightarrow$ y $\leq$ 50 ...(iii)
100 - (x + y) $\geq$ 0 $\Leftrightarrow$ x + y $\leq$ 100 ...(iv)
x + y - 60 $\geq$ 0 $\Leftrightarrow$ x + y $\geq$ 60 ...(v)
x $\geq$ 0, y $\geq$ 0 ...(vi)
सर्वप्रथम, रेखा x + y = 100 का ग्राफ खींचते हैं।
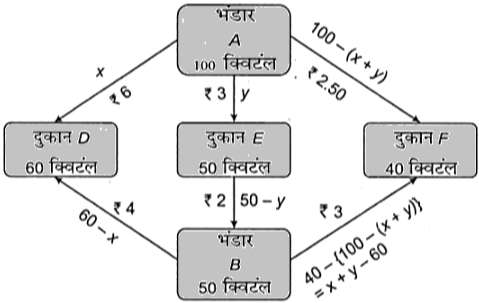
अतः हमको उद्देश्य फलन
Z = 6x + 3y + 2.50(100 - x - y) + 4(60 - x) + 2(50 - y) + 3(x + y) - 60)
= 6x + 3y + 250 - 2.5x - 2.5y + 240 - 4x + 100 - 2y + 3x + 3y - 180
= 2.50x + 1.50y + 410 ...(i)
का निम्नतम मान निम्न व्यवरोधों के अंतर्गत ज्ञात करना है।
60 - x $\geq$ 0 $\Leftrightarrow$ x $\leq$ 60 ...(ii)
50 - y $\geq$ 0 $\Leftrightarrow$ y $\leq$ 50 ...(iii)
100 - (x + y) $\geq$ 0 $\Leftrightarrow$ x + y $\leq$ 100 ...(iv)
x + y - 60 $\geq$ 0 $\Leftrightarrow$ x + y $\geq$ 60 ...(v)
x $\geq$ 0, y $\geq$ 0 ...(vi)
सर्वप्रथम, रेखा x + y = 100 का ग्राफ खींचते हैं।
| x | 0 | 100 |
| y | 100 | 0 |
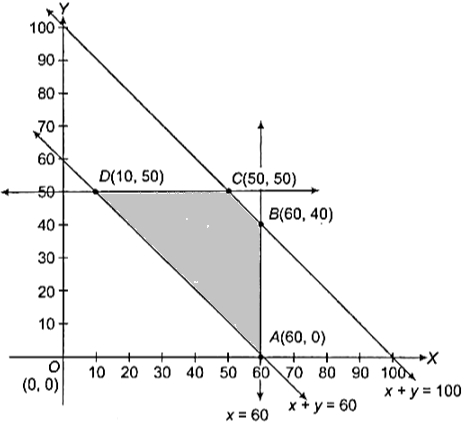
(0, 0) असमिका x + y $\leq$ 100 में रखने पर,
0 + 0 $\leq$ 100 $\Rightarrow$ 0 $\leq$ 100 (जोकि सत्य है)
अतः अर्द्धतल मूलबिंदु की ओर है।
अब, रेखा x = 60 का ग्राफ खींचते है।
(0, 0) असमिका x $\leq$ 60 में रखने पर, 0 $\leq$ 60 (जोकि सत्य है)
अतः अर्द्धतल मूलबिंदु की ओर होगा।
अब; रेखा x + y = 60 का ग्राफ खींचते हैं।
| x | 0 | 60 |
| y | 60 | 0 |
(0, 0) असमिका x + y $\geq$ 60 में रखने पर, 0 + 0 $\geq$ 60 $\Rightarrow$ 0 $\geq$ 60 (जोकि असत्य है)
अतः अर्द्धतल मूलबिंदु के विपरित ओर होगा।
अब, रेखा y = 50 का ग्राफ खींचते हैं।
(0, 0) असमिका y $\leq$ 50 में रखने पर 0 $\leq$ 50 प्राप्त होता है। (जोकि सत्य है)
अतः अर्द्धतल मूलबिंदु की ओर होगा। चूँकि x, y $\geq$ 0, अतः सुसंगत क्षेत्र प्रथम चतुर्थांश में स्थित होगा। समीकरणों के प्रतिच्छेद बिंदु A(60, 0), B(60, 40), C(50, 50) तथा D(10, 50) प्राप्त होते हैं। अतः सुसंगत क्षेत्र ABCDA है।
सुसंगत क्षेत्र के शीर्ष बिंदु A(60, 0), B(60, 40), C(50, 50) तथा D(10, 50) हैं। इन शीर्ष बिंदुओं पर Z का मान निम्न है।
| शीर्ष बिंदु | Z = 2.5x + 1.5y + 410 |
| A(60, 0) | 560 |
| B(60, 40) | 620 |
| C(50, 50) | 610 |
| D(10, 50) | 510 $\rightarrow$ निम्नतम |
Z का निम्नतम मान बिंदु D(10, 50) पर 510 है। अतः भंडार A से दुकान D, E तथा F को क्रमशः 10 क्विंटल, 50 क्विंटल तथा 40 क्विंटल अन्न उपलब्ध कराया जाता है तथा B से दुकान E तथा F का क्रमशः 50 क्विंटल, 0 क्विंटल तथा 0 क्विंटल अन्न उपलब्ध कराया जाता है, तो निम्नतम लागत ₹ 510 होती है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1आलेखीय विधि से निम्न समस्या को हल कीजिए:View Solution
निम्न व्यवरोधों के अंतर्गत
x + 3y $\leq$ 60 ...(i)
x + y $\geq$ 10 ...(ii)
x $\leq$ y ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv)
Z = 3x + 9y का न्यूनतम और अधिकतम मान ज्ञात कीजिए। - 2View Solutionएक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है। प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है। एक लैंप के निर्माण में 2 घंटे रगड़ने/काटने और 3 घंटे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घंटा रगडने/काटने और 2 घंटे स्प्रेयर की आवश्यकता होती है। स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घंटे और रगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घंटे के लिए उपलब्ध है। एक लैंप की बिक्री पर ₹5 और एक शेड की बिक्री पर ₹3 का लाभ होता है। यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते है, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
- 3ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = -3x + 4y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 8, 3x + 2y $\leq$ 12, x $\geq$ 0, y $\geq$ 0 - 4दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + y का अधिकतमीकरण कीजिए:
x - y $\leq$ -1, -x + y $\leq$ 0, x, y $\geq$ 0 - 5View Solutionएक तेल कारखाने में दो डिपो A तथा B हैं, जिनकी क्षमताएँ क्रमशः 7000 लिटर और 4000 लिटर की हैं। कारखाने द्वारा तीन पेट्रोल पंपों D, E और F के लिए आपूर्ति करनी है, जिनकी आवश्यकताएँ क्रमशः 4500 लिटर, 3000 लिटर और 3500 लिटर की है। डिपो से पेट्रोल पंपों की दूरियाँ (km में) निम्नांकित सारणी के अनुसार है:
दूरियाँ (km में) को/से A B D 7 3 E 6 4 F 3 2 यह मानते हुए कि परिवहन व्यय प्रति 10 लिटर पर प्रति किलोमीटर 1 रुपया है, ज्ञात कीजिए कि कैसी आपूर्ति योजना अपनाई जाए, जिससे परिवहन व्यय का न्यूनतमीकरण हो जाए? न्यूनतम व्यय क्या है?
- 6View Solutionएक आहारविद् दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है। भोज्य P का प्रत्येक पैकेट (जिसमें 30 ग्राम अंतर्विष्ट है) में कैल्शियम के 12 मात्रक लौह तत्व के 4 मात्रक, कोलेस्ट्रोल के 6 मात्रक और विटामिन A के 6 मात्रक अंतर्विष्ट हैं जबकि उसी मात्र के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतर्विष्ट है। आहार में कम से कम 240 मात्रक कैल्शियम, लौह तत्व के कम से कम 460 मात्रक, और कोलेस्ट्रोल के अधिक से अधिक 300 मात्रक अपेक्षित हैं। प्रत्येक भोज्य के कितने पैकेटों का उपयोग किया जाए ताकि आहार में विटामिन A की आहार में विटामिन A की मात्रा का अधिकतमीकरण करने के लिए प्रत्येक भोज्य के कितने पैकेटों का उपयोग होना चाहिए? आहार में विटामिन A की अधिकतम मात्रा क्या है?
- 7View Solutionएक फल उत्पादक अपने बाग में दो प्रकार के खादों P ब्रांड और Q ब्रांड का उपयोग कर सकता है। मिश्रण के प्रत्येक थैले में नाइट्रोजन, फास्फोरिक अम्ल, पोटाश और क्लोरीन की मात्रा (किग्रा में) सारणी में दिया गया हैं परीक्षण संकेत देते हैं कि बाग को कम-से-कम 250 किग्रा फास्फोरिक अम्ल, कम-से-कम 270 किग्रा पोटाश और क्लोरीन की अधिक-से-अधिक 310 किग्रा की आवश्यकता है।
यदि उत्पादक बाग में मिलाई जाने वाली नाइट्रोजन की मात्रा का अधिकतमीकरण चाहता है, तो मिश्रण के कितने थैलों को मिलाया जाना चाहिए। मिलाई जाने वाली नाइट्रोजन की अधिकतम मात्रा क्या है?
kg प्रति थैला ब्राँड P ब्राँड Q नाइट्रोजन 3 3.5 फास्फोरिक अम्ल 1 2 पोटाश 3 1.5 क्लोरीन 1.5 2 - 8आलेख द्वारा निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न व्यवरोधों के अंतर्गत
x + y $\leq$ 50 ...(i)
3x + y $\leq$ 90 ...(ii)
x $\geq$ 0, y $\geq$ 0 ...(iii)
Z = 4x + y का अधिकतम मान ज्ञात कीजिए। - 9View Solutionएक आहारविद् दो प्रकार के भोज्यों X और Y को इस प्रकार मिलाना चाहता है कि मिश्रण में विटामिन A, की कम से कम 10 मात्रक, विटामिन B की कम से कम 12 मात्रक और विटामिन C की 8 मात्रक हों 1 kg भोज्यों में विटामिनों की मात्रा निम्नलिखित सारणी में दी गई है।
भोज्य विटामिन A विटामिन B विटामिन C X 1 2 3 Y 2 2 1 भोज्य X के 1 kg का मूल्य ₹16 और भोज्य y के 1 kg का मूल्य ₹20 है। वांछित आहार के लिए मिश्रण का न्यूनतम मूल्य ज्ञात कीजिए।
- 10View Solutionएक खिलौना कंपनी, A और B दो प्रकार की गुड़ियों का निर्माण करती है। मार्किट परीक्षणों तथा उपलब्ध संसाधनों से संकेत मिलता है कि सम्मिलित उत्पादन स्तर प्रति सप्ताह 1200 गुड़ियों से अधिक नहीं होना चाहिए और B प्रकार की गुड़ियों की अधिक से अधिक माँग A प्रकार की गुड़ियों की आधी है। इसके अतिरिक्त A प्रकार की गुड़ियों का उत्पादन स्तर दूसरे प्रकार की गुड़ियों के उत्पादन स्तर के तीन गुने से 600 नग अधिक है। यदि कंपनी A और B प्रत्येक गुड़िया पर क्रमशः ₹12 और ₹16 का लाभ कमाती है, लाभ का अधिकतमीकरण करने के लिए प्रत्येक के कितने नगों का साप्ताहिक उत्पादन करना चाहिए।